二次函数与反比例函数—浙教版数学九（上）知识点训练

试卷更新日期：2024-11-23 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 反比例函数 $y = \frac{k}{x}$ 与二次函数 $y = - k x^{2} + k (k \neq 0)$ 在同一平面直角坐标系中的大致图像是（）

A、 B、 C、 D、

查看试题解析
2. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象如图所示，那么二次函数 $y = 2 k x^{2} - 3 x + k^{2}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
3. 二次函数 y=ax²+bx+c(a≠0) 的图象如图所示，则一次函数 y=bx+b²-4ac 与反比例函数 y= $\frac{a + b + c}{x}$ 在坐标系内的图象大致为（）

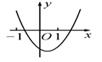A、 B、 C、 D、

查看试题解析
4. 如图，二次函数y＝ax²+bx+c与反比例函数y＝ $\frac{k}{x}$ 的图象相交于点A（﹣1，y₁）、B（1，y₂）、C（3，y₃）三个点，则不等式ax²+bx+c＞ $\frac{k}{x}$ 的解是．

查看试题解析
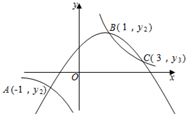5. 甲、乙两人研究二次函数 $y = a x^{2} - 4 a x + 3 (a \neq 0)$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ ，甲说：“二次函数图象一定过第一象限的一个定点.”乙说：“二次函数图象的顶点及这个定点都在该反比例函数图象上.”若甲、乙两人的描述正确，则a的值为.

查看试题解析
6. 若二次函数 $y = - 3 {(x - m)}^{2} - 4$ 的对称轴是直线 $x = 1$ ，则反比例函数 $y = \frac{m}{x}$ 经过第象限．

查看试题解析
7. 已知二次函数y=a(x+3)²+4的图象是由函数y=0.5x²的图象经平移得到，且与反比例函数y= $\frac{m}{x}$ 的图象交于点(1，n)，求a，m，n的值．

查看试题解析
8. 如图，二次函数图象的顶点为（-1，1），且与反比例函数的图象交于点A（-3，-3）

(1)、求二次函数与反比例函数的解析式；

(2)、判断原点（0，0）是否在二次函数的图象上，并说明理由；

(3)、根据图象直接写出二次函数的值小于反比例函数的值时自变量x的取值范围．

查看试题解析
9. 如图，二次函数 $y = a x^{2} + b x + c$ 图像的顶点为 $(- 1 ， 1)$ ，且与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像交于点 $A (- 3 ， - 3)$

(1)、判断原点 $(0 ， 0)$ 是否在二次函数的图象上，并说明理由；

(2)、根据图像，直接写出关于x的不等式 $a x^{2} + b x + c < \frac{k}{x}$ 的解.

查看试题解析
10. 如图，曲线BC是反比例函数 $y = \frac{k}{x}$ $(2 \leq x \leq 4)$ 的一部分，其中B（2，2-m），C（4，-m），抛物线 $y = - x^{2} + 2 b x$ 的顶点记作A．

(1)、求k的值；

(2)、甲同学说，点A可以与点B重合；而乙同学说，点A也可以与点C重合，甲、乙的说法对吗？请说明理由．

查看试题解析

二、能力提升

11. 如图，一组x轴正半轴上的点 $B_{1}$ ， $B_{2}$ ， … $B_{n}$ 满足条件 $O B_{1} = B_{1} B_{2} = B_{2} B_{3} ⋯ = B_{n - 1} B_{n} = 2$ ，抛物线的顶点 $A_{1}$ ， $A_{2}$ ， … $A_{n}$ 依次是反比例函数 $y = \frac{9}{x}$ 图象上的点，第一条抛物线以 $A_{1}$ 为顶点且过点O和 $B_{1}$ ；第二条抛物线以 $A_{2}$ 为顶点且经过点 $B_{1}$ 和 $B_{2}$ ；…第n条抛物线以 $A_{n}$ 为顶点且经过点 $B_{n - 1}$ ， $B_{n}$ ，依次连结抛物线的顶点和与x轴的两个交点，形成 $△ O A_{1} B_{1}$ 、 $△ B_{1} A_{2} B_{2}$ 、…、 $△ B_{n - 1} A_{n} B_{n}$ ．请写出所有满足三角形面积为整数的n的值．

查看试题解析
12. 如图，对称轴为x=2的抛物线y= ${ax}^{2} + bx (a \neq 0) 与 x 轴交于原点 O 与点 A ，与$ 反比例函数 $y = \frac{b}{x}$ （x＞0）交于点B，过点B作x轴的平行线，交y轴于点C，交反比例函数 $y = \frac{a}{x}$ 于点D，连接OB、OD。则下列结论中：①ab＞0；②方程 ${ax}^{2} + bx = 0$ 的两根为0，4；③3a+b＜0；④tan∠BOC=4tan∠COD不符合题意的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
13. 如图，在平面直角坐标系中，点 $A (2 ， 3)$ 为二次函数 $y = a x^{2} + b x - 2 (a \neq 0)$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限的交点，已知该抛物线 $y = a x^{2} + b x - 2 (a \neq 0)$ 与 $x$ 轴正、负半轴分别交于点 $E$ 、点 $D$ ，交 $y$ 轴负半轴于点 $B$ ，且 $\tan ∠ A D E = \frac{1}{2}$ ．

(1)、求二次函数和反比例函数的表达式；

(2)、已知点 $M$ 为抛物线上一点，且在第三象限，顺次连接点 $D 、 M 、 B 、 E$ ，求四边形 $D M B E$ 面积的最大值．

查看试题解析
14. 在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x}$ 的图象经过点A（1，4），B（m，n）．

(1)、求反比例函数 $y = \frac{k}{x}$ 的解析式；

(2)、若二次函数 $y = {(x - 1)}^{2}$ 的图象经过点B，求代数式 $\frac{m^{2} - 2 m - 3}{4} - \frac{n + 1}{m n}$ 的值；

(3)、若反比例函数 $y = \frac{k}{x}$ 的图象与二次函数 $y = a {(x - 1)}^{2}$ 的图象只有一个交点，且该交点在直线y＝x的下方，结合函数图象，求a的取值范围．

查看试题解析

三、拓展探索

15. 若一次函数 $y = m x + n$ 与反比例函数 $y = \frac{k}{x}$ 同时经过点 $P (x ， y)$ 则称二次函数 $y = m x^{2} + n x - k$ 为一次函数与反比例函数的“共享函数”，称点P为共享点．

(1)、判断 $y = x - 2$ 与 $y = \frac{3}{x}$ 是否存在“共享函数”，如果存在，请求出“共享点”．如果不存在，请说明理由；

(2)、已知：整数m，n，t满足条件 $t < n < 8 m$ ，并且一次函数 $y = (1 + n) x + 2 m + 2$ 与反比例函数 $y = \frac{2020}{x}$ 存在“共享函数” $y = (m + t) x^{2} + (10 m - t) x - 2020$ ，求m的值．

(3)、若一次函数 $y = x + m$ 和反比例函数 $y = \frac{m}{x}$ 在自变量x的值满足的 $m \leq x \leq m + 6$ 的情况下．其“共享函数”的最小值为3，求其“共享函数”的解析式．

查看试题解析