二次函数与分段函数—浙教版数学九(上)知识点训练
试卷更新日期:2024-11-23 类型:复习试卷
一、选择题
-
1. 现有函数如果对于任意的实数 , 直线与函数的图象总有交点,那么实数的取值范围是( )A、 B、 C、 D、2. 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
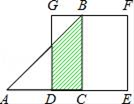 A、
A、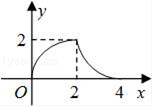 B、
B、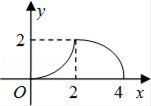 C、
C、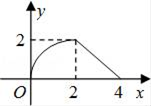 D、
D、 3. 如图,正方形ABCD的边长是4,点E , F分别是AB , AD的中点,点P , Q为正方形ABCD边上的两个动点,点P从点D出发,沿匀速运动,到达点C时停止运动;同时,点Q从点E出发,沿匀速运动,动点P , Q速度的大小相同.设点P运动的路程为x , 的面积为y , 下列图象中能反映y与x之间函数关系的是( )
3. 如图,正方形ABCD的边长是4,点E , F分别是AB , AD的中点,点P , Q为正方形ABCD边上的两个动点,点P从点D出发,沿匀速运动,到达点C时停止运动;同时,点Q从点E出发,沿匀速运动,动点P , Q速度的大小相同.设点P运动的路程为x , 的面积为y , 下列图象中能反映y与x之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′= ,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )A、
4. 在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′= ,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
5. 若函数y= , 则当函数值y=8时,自变量x的值等于.6. 在平面直角坐标系xOy中,函数 (其中 )的图象记为W,图象W经过点 ,则n的值为 .7. 定义一个运算: , 如 . 用表示大于最小整数,如 . 按照上述规定,若整数满足 , 则的值是 .
三、解答题
-
8. 某商店销售某种商品的进价为每件 30 元, 这种商品在近 60 天中的日销售价与日销售量的相关信息如下表:
时间: 第 (天)
日销售价 (元/件 )
50
日销售量 (件)
为整数)
设该商品的日销售利润为 元.
(1)、 直接写出 与 的函数关系式(2)、该商品在第几天的日销售利润最大? 最大日销售利润是多少?9. 如图,在△ABC中,∠C=90°,∠B=30°,AC=3cm , AD是△ABC的角平分线.动点P从点A出发,以的速度沿折线AD﹣DB向终点B运动.过点P作PQ∥AB , 交AC于点Q , 以PQ为边作等边三角形PQE , 且点C , E在PQ同侧.设点P的运动时间为t(s)(t>0),△PQE与△ABC重合部分图形的面积为S(cm2). (1)、当点P在线段AD上运动时,判断△APQ的形状(不必证明),并直接写出AQ的长(用含t的代数式表示).(2)、当点E与点C重合时,求t的值.(3)、求S关于t的函数解析式,并写出自变量t的取值范围.10. 在平面直角坐标系中,二次函数的图象经过原点.
(1)、当点P在线段AD上运动时,判断△APQ的形状(不必证明),并直接写出AQ的长(用含t的代数式表示).(2)、当点E与点C重合时,求t的值.(3)、求S关于t的函数解析式,并写出自变量t的取值范围.10. 在平面直角坐标系中,二次函数的图象经过原点. (1)、求该二次函数的解析式以及顶点坐标;(2)、将该二次函数的图象在y轴左侧的部分记作W,将W绕原点旋转得到 , W与组成一个新函数的图象.
(1)、求该二次函数的解析式以及顶点坐标;(2)、将该二次函数的图象在y轴左侧的部分记作W,将W绕原点旋转得到 , W与组成一个新函数的图象.①若点在该新函数图象上,求b的值;
②若点是新函数图象上两点,若存在 , 使得 , 直接写出m的取值范围.
11. 如图,二次函数y=﹣x2+bx+3交x轴于A(﹣1,0)和B , 交y轴于C . (1)、求b的值.(2)、M为函数图象上一点,满足∠MAB=∠ACO , 求M点的横坐标.(3)、将二次函数沿水平方向平移,新的图象记为L , L与y轴交于点D , 记DC=d , 记L顶点横坐标为n .
(1)、求b的值.(2)、M为函数图象上一点,满足∠MAB=∠ACO , 求M点的横坐标.(3)、将二次函数沿水平方向平移,新的图象记为L , L与y轴交于点D , 记DC=d , 记L顶点横坐标为n .①求d与n的函数解析式.
②记L与x轴围成的图象为U , U与△ABC重合部分(不计边界)记为W , 若d随n增加而增加,且W内恰有2个横坐标与纵坐标均为整数的点,直接写出n的取值范围.
12. 对某一个函数给出如下定义:若存在实数 , 对于任意的函数值 , 都满足 , 则称这个函数是有界函数,在所有满足条件的中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
(1)分别判断函数和是不是有界函数?若是有界函数,求其边界值;
(2)若函数的边界值是2,且这个函数的最大值也是2,求的取值范围;
(3)将函数的图象向下平移个单位,得到的函数的边界值是 , 当在什么范围时,满足?
13. 对于函数定义变换:当y≥0时,函数值不变;当y<0时,我们把这种变换称为函数的“关联变换”,变换后的函数称为原函数的“关联函数”如:一次函数y=x﹣1,关联函数为 , 这个关联函数的转折点是(1,0).
(1)、已知一次函数y=2x﹣3,请直接写出它的“关联函数”的解析式.(2)、已知二次函数y=﹣2x﹣3,点(a,4)在它的“关联函数”的图象上,求a的值.(3)、在平面直角坐标系内,有点M(﹣1,1)、N(3,1),二次函数y=﹣2x+a的关联函数与线段MN恰有两个公共点.求a的取值范围14. 在函数学习中,我们经历了“确定函数表达式画函数图象利用函数图象研究函数性质利用图象解决问题”的学习过程.以下是我们研究函数的性质及其应用的部分过程,请你按要求完成下列问题(1)、列表:函数自变量的取值范围是全体实数,下表列出了变量与的几组对应数值:根据表格中的数据直接写出与的函数解析式及对应的自变量的取值范围;
(2)、描点、连线:在右侧的平面直角坐标系中,画出该函数的图象,并写出该函数的一条性质: ▲ ;(3)、已知函数的图象如图,结合函数图象,请直接写出当时,自变量的值.结果保留位小数,误差不超过 15. 如图所示,图象G由图象和组成,其中图象是函数的图象,图象是函数的图象.
15. 如图所示,图象G由图象和组成,其中图象是函数的图象,图象是函数的图象. (1)、若点在图象G上,求p的值;(2)、已知直线l与x轴平行,且与图象G有三个不同的交点,从左至右依次为点A、B、C , 若 , 求点C的坐标;(3)、当图象G上的点满足时,记此时x的取值范围为M . 设 , 若在M中总存在 , 使得 , 求此时实数m的取值范围.16. 如图,已知经过点和的抛物线与轴交于点 , 过点作轴交抛物线于点 .
(1)、若点在图象G上,求p的值;(2)、已知直线l与x轴平行,且与图象G有三个不同的交点,从左至右依次为点A、B、C , 若 , 求点C的坐标;(3)、当图象G上的点满足时,记此时x的取值范围为M . 设 , 若在M中总存在 , 使得 , 求此时实数m的取值范围.16. 如图,已知经过点和的抛物线与轴交于点 , 过点作轴交抛物线于点 .

(备用图)
(1)、请用含的代数式表示和点的坐标;(2)、设直线垂直平分 , 垂足为 , 交该抛物线的对称轴于点 , 连接 , , , 求的值;(3)、若在(2)的条件下,若点是抛物线上在轴右侧的一个动点,其横坐标为 , 点到抛物线对称轴和直线的距离分别是 , , 且 , ①求关于的函数解析式;②当时,直接写出的取值范围.17. 如图1,在平面直角坐标系中,O为坐标原点,抛物线与x轴交于点 , 两点,交y轴于点C . (1)、求抛物线的解析式;(2)、如图2,连接BC , 点P为BC下方抛物线上一点,连接PB , PC , 若设的面积为S , 点P的横坐标为t , 求s与t的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,如图3,点Q为BC上一点,连接PQ并延长交x轴于点E , 延长PB至点D , 连接QD交x轴于点M , , 点M为QD中点,连接AC , 点F在AC上,连接EF , 交BC于点K , 连接EK , EH平分交FK于点H , 交EF于点T , 于点G , 若 , , 求点P的坐标.18. 定义:经过函数图象上的一点作x轴的平行线,将平行线上方的图像沿平行线向下翻折形成新的函数图象,我们把满足这种情况的函数图象称为经过这一点的“折叠函数”.(1)、【基本应用】
(1)、求抛物线的解析式;(2)、如图2,连接BC , 点P为BC下方抛物线上一点,连接PB , PC , 若设的面积为S , 点P的横坐标为t , 求s与t的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,如图3,点Q为BC上一点,连接PQ并延长交x轴于点E , 延长PB至点D , 连接QD交x轴于点M , , 点M为QD中点,连接AC , 点F在AC上,连接EF , 交BC于点K , 连接EK , EH平分交FK于点H , 交EF于点T , 于点G , 若 , , 求点P的坐标.18. 定义:经过函数图象上的一点作x轴的平行线,将平行线上方的图像沿平行线向下翻折形成新的函数图象,我们把满足这种情况的函数图象称为经过这一点的“折叠函数”.(1)、【基本应用】(ⅰ)如图,点、、均在直线l上.

①请使用无刻度的直尺和圆规作出经过点C的“折叠函数”与x轴的交点D(异于点A);
②求出经过点A、C、D的二次函数表达式;
(ⅱ)在(ⅰ)的条件下,点为二次函数图象上一动点,若经过点P的“折叠函数”与x轴至少有3个交点,求a的取值范围.
(2)、【创新应用】如果反比例函数的图像上有一点 , 则经过点M的“折叠函数”与x轴的交点坐标为 .