二次函数与不等式（组）—浙教版数学九（上）知识点训练

试卷更新日期：2024-11-23 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，二次函数y＝ax²+bx+c的图象的对称轴为x＝- $\frac{1}{2}$ ，且经过点（-2，0），（x₁ ， y₁），（x₂ ， y₂），下列说法正确的是（）

A、bc＞0 B、当x₁＞x₂≥- $\frac{1}{2}$ 时，y₁＞y₂ C、a＝2b D、不等式ax²+bx+c＜0的解集是-2＜x＜ $\frac{3}{2}$

查看试题解析
2. 已知函数 $y_{1} = x^{2}$ 与函数 $y_{2} = - \frac{1}{2} x + 3$ 的图象大致如图.若 $y_{1} < y_{2} ，$ 则自变量 $x$ 的取值范围是（　　）.

A、 $- \frac{3}{2} < x < 2$ B、 $x > 2 或 x < - \frac{3}{2}$ C、 $- 2 < x < \frac{3}{2}$ D、 $x ⟨- 2 或 x⟩ \frac{3}{2}$

查看试题解析
3. 已知二次函数 $y = x^{2} - 2 x - 3$ ，若 $y > - 3$ ，则自变量 $x$ 的取值范围是（）

A、 $x < 0$ 或 $x > 2$ B、 $x < 1$ 或 $x > 3$ C、 $0 < x < 2$ D、 $1 < x < 3$

查看试题解析
4. 已知抛物线y＝x²+bx的对称轴为直线x＝3，则关于x的不等式x²+bx＜﹣8的取值范围是（）

A、1＜x＜5 B、2＜x＜4 C、0＜x＜6 D、﹣1＜x＜7

查看试题解析
5. 如图抛物线y＝ax²+bx+c的对称轴是x＝﹣1，与x轴的一个交点为（﹣5，0），则不等式ax²+bx+c＞0的解集为.

查看试题解析
6. $y = - 3 x^{2} + b x + c$ 经过点 $A (0 ， 2) ， B (4 ， 2)$ ，则不等式 $- 3 x^{2} + b x + c < 2$ 的解集是．

查看试题解析
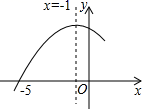7. 已知二次函数y＝x²＋bx＋c经过A(1，1)和B(－1，－3)，二次函数与一次函数y＝－x－2交于C ， D两点．

(1)、求二次函数的解析式．

(2)、求三角形BCD的面积．

(3)、结合图象直接写出不等式x²＋bx＋c＞－x－2的解集．

查看试题解析
8. 在平面直角坐标系中，设二次函数 $y = a x^{2} - (2 a - 2) x - 3 a - 1$ ，实数 $a \neq 0$

(1)、若二次函数图象经过点（-2，-10），求这个二次函数的解析式及顶点坐标：

(2)、若二次函数图象上始终存在两个不同点，这两个点关于原点对称，求a的取值范围；

(3)、若 $a > 0$ ，设点 $M (m ， y_{1})$ ， $N (n ， y_{2})$ 是二次函数图象上两个不同点，且 $m + n + 2 = 0$ ，求证： $y_{1} + y_{2} > - 6$ .

查看试题解析

二、能力提升

9. 已知二次函数 $y = a x^{2} + b x + c$ 的图象过 $A (x_{1} ， y_{1})$ ， $B (1 - m ， n)$ ， $C (x_{2} ， y_{2})$ ， $D (m + 5 ， n)$ ，若 $| x_{1} - 3 | \geq | x_{2} - 3 |$ ，则下列表达式正确的是（）

A、对于任意 $a (a \neq 0)$ ， $a (y_{1} - y_{2}) > 0$ 恒成立 B、不存在实数 $a$ ，使得 $y_{1} - y_{2} > 0$ 成立 C、存在实数 $a$ ，使得 $a (y_{1} - y_{2}) < 0$ 成立 D、对于任意 $a (a \neq 0)$ ， $y_{1} - y_{2} > 0$ 恒成立

查看试题解析
10. 汽车在刹车后，由于惯性作用还要继续向前滑行一段距离才能停下，我们称这段距离为“刹车距离”，刹车距离往往跟行驶速度有关，在一个限速35km/h的弯道上，甲、乙两辆汽车相向而行，发现情况不妙，同时刹车，最后还是相撞了事发后，交警现场测得甲车的刹车距离略超过12m，乙车的刹车距离略超过10m，又知甲、乙两种车型的刹车距离s（m）与车速x（km/h）的关系大致如下：S_甲 $= \frac{1}{100} x^{2} + \frac{1}{10}$ ，S_乙 $= \frac{1}{200} x^{2} + \frac{1}{20} x$ .由此可以推测（）

A、甲车超速 B、乙车超速 C、两车都超速 D、两车都未超速

查看试题解析
11. 如图，已知y＝ $\frac{6}{x}$ 与y＝x²﹣7的图象的交点A（﹣2，﹣3），B（﹣1，﹣6），C（3，2），则不等式x²＞ $\frac{6}{x}$ +7的解集为（）

A、x＜﹣2或x＞3 B、﹣2＜x＜﹣1或0＜x＜3 C、﹣2＜x＜﹣1或x＞3 D、x＜﹣2或﹣1＜x＜0或x＞3

查看试题解析
12. 已知二次函数y=x²-4x+3和一次函数y=-px+p，若对于满足0≤p≤4的一切实数，不等式x²-4x+3>-px+p恒成立，则实数x的取值范围是（）

A、x>1 B、1<x<3 C、-1<x<3 D、x<-1或x>3

查看试题解析
13. 抛物线 $y = a x^{2} + b x + c (a ， b ， c 为常数，且 a \neq 0)$ 交 $x$ 轴于A（-1，0），B（2，0）两点，则不等式 $x^{2} + \frac{b}{a} x + \frac{c}{a} > 0$ 的解为．

查看试题解析
14. 对于二次函数 $y = a x^{2} + b x + c$ ，规定函数 $y = {\begin{array}{l} a x^{2} + b x + c (x \geq 0) \\ - a x^{2} - b x - c (x < 0) \end{array}$ 是它的相关函数.已知点 $M$ ， $N$ 的坐标分别为 $(- \frac{1}{2} ， 1)$ ， $(\frac{9}{2} ， 1)$ ，连接 $M N$ ，若线段 $M N$ 与二次函数 $y = - x^{2} + 4 x + n$ 的相关函数的图象有两个公共点，则 $n$ 的取值范围为．

查看试题解析
15. 已知抛物线 $y = \frac{1}{2} x^{2} - m x + m^{2}$ 经过点 $P (2 ， k)$ .请解决下列问题：

(1)、点 $A (a ， n) ， B (b ， n)$ 分别落在抛物线 $y = \frac{1}{2} x^{2} - m x + m^{2}$ 上，且 $a + b = 4$ ，求 $k$ 的值.

(2)、当 $- 2 ⩽ m ⩽ 1$ 时，
①求 $k$ 的取值范围.
②若 $- 2 ⩽ x ⩽ 1 ， y_{最大} - y_{最小} = 4$ ，求 $m$ 的值.

查看试题解析
16. 已知，点M为二次函数y=-x²+2bx-b²+4b+1图象的顶点，直线y=mx+5分别交x轴正半轴和y轴于点A，B．

(1)、判断顶点M是否在直线y=4x+1上，并说明理由；

(2)、如图1，若二次函数图象也经过点A，B，且mx+5＞-x²+2bx-b²+4b+1，结合图象，求x的取值范围；

(3)、如图2，点A坐标为(5，0)，点M在△AOB内，若点C( $\frac{1}{4}$ ， y₁)，D( $\frac{3}{4}$ ， y₂)都在二次函数图象上，试比较y₁与y₂的大小．

查看试题解析

三、拓展创新

17. 请阅读下列解题过程：解一元二次不等式：x²-2x-3＜0．

解：设x²-2x-3＝0，解得：x₁＝-1，x₂＝3，

则抛物线y＝x²-2x-3与x轴的交点坐标为（-1，0）和（3，0）．

画出二次函数y＝x²-2x-3的大致图象（如图所示）．

由图象可知：当-1＜x＜3时函数图象位于x轴下方，此时y＜0，即x²-2x-3＜0．

所以一元二次不等式x²-2x-3＜0的解集为：-1＜x＜3．

通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：

(1)、上述解题过程中，渗透了下列数学思想中的和 .（只填序号）

①转化思想；②分类讨论思想；③数形结合思想．

(2)、用类似的方法解一元二次不等式：-x²+2x＞0．

(3)、某“数学兴趣小组”根据以上的经验，对函数y＝-（x-1）（|x|-3）的图象和性质进行了探究，探究过程如下，请补充完整：

①自变量x的取值范围是▲；x与y的几组对应值如表，其中m＝▲ ．

x	…	-4	-3	-2	-1	0	1	2	3	4	…
y	…	5	0	-3	m	-3	0	1	0	-3	…

②如图，在直角坐标系中画出了函数y＝-（x-1）（|x|-3）的部分图象，用描点法将这个图象补画完整．

③结合函数图象，解决下列问题：

解不等式：-3≤-（x-1）（|x|-3）≤0．

查看试题解析

18. 新定义：我们把抛物线 $y_{1} = a x^{2} + b x + c$ 与抛物线 $y_{2} = b x^{2} + a x + c$ (其中 $a b \neq 0$ )称为“关联抛物线”.例如：抛物线 $y_{1} = 3 x^{2} + 4 x + 2$ 的“关联抛物线”为 $y_{2} = 4 x^{2} + 3 x + 2$ .已知抛物线 $C_{1} ： y_{1} = 2 a x^{2} + a x + a - 2 (a \neq 0)$ 的“关联抛物线”为 $C_{2}$ .

(1)、写出抛物线 $C_{2}$ 的函数表达式(用含 $a$ 的式子表示) $y_{2} =$ ，顶点坐标为.

(2)、对于 $C_{1}$ 和 $C_{2}$ ，当 $y_{1} > y_{2}$ 时，求 $x$ 的取值范围.

(3)、若 $a > 0$ ，当 $a - 3 ⩽ x ⩽ a - 1$ 时， $C_{2}$ 的最大值与最小值的差为2a，求 $a$ 的值.

查看试题解析