二次函数图象与坐标轴—浙教版数学九（上）知识点训练

试卷更新日期：2024-11-23 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 抛物线y＝x²+4x+4与x轴的交点个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 二次函数 $y = c x^{2} - 4 x + 2 c$ 的图象的最高点在 $x$ 轴上，则 $c$ 的值为（）

A、 $\sqrt{2}$ B、 $- \sqrt{2}$ C、 $\pm \sqrt{2}$ D、 $\pm 2$

查看试题解析
3. 二次函数 $y = 2 x^{2} + 5 x - 3$ 与y轴的交点是（）

A、 $(\frac{1}{2}, 0)$ B、 $(0, 3)$ C、 $(0, - 3)$ D、 $(- 3, 0)$

查看试题解析
4. 已知二次函数y=ax²+bx+1的图象与x轴没有交点，且过点A(-2，y₁)，B(-3，y₂)，C(1，y₂)，D( $\sqrt{3}$ ， y₃)，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₂>y₁>y₃ B、y₃>y₂>y₁ C、y₁>y₃>y₂ D、y₁>y₂>y₃

查看试题解析
5. 二次函数 $y = 2 x^{2} - 8 x + m$ 的图象与 $x$ 轴有两个交点，若其中一个交点的坐标为 $(- 1，0)$ ，则另一个交点坐标为（）

A、 $(- 3，0)$ B、 $(3，0)$ C、 $(5，0)$ D、 $(9，0)$

查看试题解析
6. 已知二次函数 $y = x^{2} + m x$ 的图象的对称轴为直线 $x = 2$ ，则抛物线 $y = x^{2} + m x$ 在 $x$ 轴上截得的线段长为（）

A、4 B、5 C、6 D、7

查看试题解析
7. 若函数y=mx²+2x+1的图象与x轴只有一个公共点，则常数m的值是．

查看试题解析
8. 抛物线y＝ax²+bx+c（a≠0）的图象与x轴交点的横坐标为-5和1，则方程ax²－bx＋c=0的解为．

查看试题解析
9. 已知抛物线y＝x²－1．

(1)、说出该抛物线的开口方向和对称轴；

(2)、设该抛物线与x轴交于点A，B，求交点A，B之间的距离．

查看试题解析
10. 已知二次函数 $y = x^{2} + a x + a$ （a为常数， $a \neq 0$ ）．

(1)、若函数经过点 $(- 2 ， 5)$ ，求二次函数的解析式和顶点坐标．

(2)、当 $0 < a < 4$ 时，求该二次函数的图象与x轴的交点个数．

(3)、设 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 是该函数图象上的两点，其中 $x_{1} < x_{2}$ ，当 $x_{1} + x_{2} > 4$ 时，都有 $y_{1} < y_{2}$ ，求a的取值范围．

查看试题解析

二、能力提升

11. 如图，已知在平面直角坐标系 $x O y$ 中，一段抛物线 $y = - x^{2} + 6 x (0 \leq x \leq 6)$ ，记为抛物线 $C_{1}$ ，它与 $x$ 轴交于点 $O$ ， $A_{1}$ ；将抛物线 $C_{1}$ 绕点 $A_{1}$ 旋转 $180 °$ 得抛物线 $C_{2}$ ，交 $x$ 轴于点 $A_{1}$ ， $A_{2}$ ；将抛物线 $C_{2}$ 绕点 $A_{2}$ ，旋转 $180 °$ 得抛物线 $C_{3}$ ，交 $x$ 轴于点 $A_{2}$ ， $A_{3}$ ；……如此进行下去，得到一条“波浪线”，若点 $M (2023 ， m)$ 在此“波浪线”上，则 $m$ 的值为（）

A、 $- 9$ B、 $- 5$ C、9 D、5

查看试题解析
12. 已知二次函数y=x²-2x+m的图象C与y轴交于点M，过点M作直线l平行于x轴，将抛物线C位于直线l下方的部分翻折至直线l上方．若变换后的图象与x轴有4个交点，则m的取值范围为（）

A、m＞—1 B、-1＜m＜0 C、-1≤m≤0 D、-1≤m＜0

查看试题解析
13. 已知函数 $y = m x^{2} + 2 x - m + 2$ 的图象与坐标轴只有两个交点，则 $m =$ ．

查看试题解析
14. 如图，抛物线 $y = \frac{1}{4} x (x - 8)$ 与x轴交于点O，E，矩形ABCD的边AB在线段OE上，点B（2，0）在点A的左侧，点C，D在抛物线上，向右平移抛物线，当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形ABCD的面积时，则抛物线平移的距离为．

查看试题解析
15. 如图是二次函数 $y = {(x + m)}^{2} + k$ 的图象，其顶点坐标为 $M (1, - 4)$ ．

(1)、求出图象与x轴的交点A，B的坐标；

(2)、在二次函数的图象上是否存在点P，使 $S_{△ P A B} = S_{△ M A B}$ ，若存在，求出P点的坐标；若不存在，请说明理由．

(3)、在y轴上存在一点Q，使得 $△ Q M B$ 周长最小，求此时构成的 $△ Q M B$ 的面积．

查看试题解析

三、拓展创新

16. 定义：若函数 $y = x_{}^{2} + b x + c$ （c≠0）与 $x$ 轴的交点A，B的横坐标为 $x_{A}^{}$ ， $x_{B}^{}$ ，与 $y$ 轴交点的纵坐标为 $y_{C}^{}$ ，若 $x_{A}^{}$ ， $x_{B}^{}$ 中至少存在一个值，满足 $x_{A}^{}$ ＝ $y_{C}^{}$ （或 $x_{B}^{}$ ＝ $y_{C}^{}$ ），则称该函数为友好函数．如图，函数 $y = x_{}^{2} + 2 x - 3$ 与 $x$ 轴的一个交点A的横坐标为-3，与y轴交点C的纵坐标为-3，满足 $x_{A}^{}$ ＝ $y_{C}^{}$ ，称 $y = x_{}^{2} + 2 x - 3$ 为友好函数．

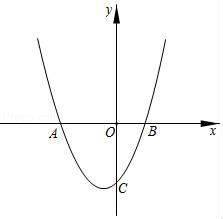(1)、判断 $y = x_{}^{2} - 5 x + 4$ 是否为友好函数，并说明理由；

(2)、请探究友好函数 $y = 2 x_{}^{2} + b x + c$ 表达式中的b与c之间的关系；

(3)、若 $y = 2 x_{}^{2} + b x + c$ 是友好函数，∠ACB为锐角，求c的取值范围．

查看试题解析
17. 在平面直角坐标系中，抛物线 $y = a x^{2} - 2 a x - 3 a (a \neq 0)$ 的顶点为P，且该抛物线与x轴交于A，B两点（点A在点B的左侧）.我们规定；抛物线与x轴围成的封闭区域称为“G区城”（不包含边界），横、纵坐标都是整数的点称为整点.

(1)、求抛物线 $y = a x^{2} - 2 a x - 3 a$ 的顶点P的坐标（用含a的代数式表示）；

(2)、如果抛物线 $y = a x^{2} - 2 a x - 3 a$ 经过（1，3）.
①求a的值
②在①的条件下，直接写出“G区域”内整点的坐标；

(3)、如果抛物线 $y = a x^{2} - 2 a x - 3 a$ 在“G区域”内有4个整点，求a的取值范围，

查看试题解析