二次函数图象共存问题—浙教版数学九(上)知识点训练
试卷更新日期:2024-11-23 类型:复习试卷
一、二次函数与一次函数图象共存
-
1. 函数与在同一平面直角坐标系中的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 2. 当ab<0时,y=ax与y=ax+b的图象大致是( )A、
2. 当ab<0时,y=ax与y=ax+b的图象大致是( )A、 B、
B、 C、
C、 D、
D、 3. 函数和在同一平面直角坐标系内的图象大致是( )A、
3. 函数和在同一平面直角坐标系内的图象大致是( )A、 B、
B、 C、
C、 D、
D、 4. 在同一直角坐标系中,一次函数和二次函数的图象大致为( )A、
4. 在同一直角坐标系中,一次函数和二次函数的图象大致为( )A、 B、
B、 C、
C、 D、
D、 5. 函数y=kx+k和函数y=﹣kx2+4x+4(k是常数,且k≠0)在同一平面直角坐标系中的图象可能是( )A、
5. 函数y=kx+k和函数y=﹣kx2+4x+4(k是常数,且k≠0)在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、二次函数与反比例函数图象共存
-
6. 若反比例函数 的图象在第二、四象限, 则二次函数 的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 7. 反比例函数 图象在二、四象限,则二次函数 的大致图象是( )A、
7. 反比例函数 图象在二、四象限,则二次函数 的大致图象是( )A、 B、
B、 C、
C、 D、
D、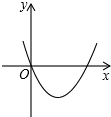 8. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )
8. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )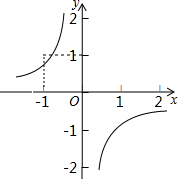 A、
A、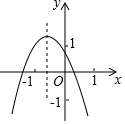 B、
B、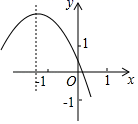 C、
C、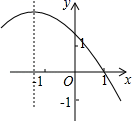 D、
D、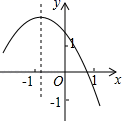 9. 反比例函数与二次函数在同一平面直角坐标系中的大致图象是( )A、
9. 反比例函数与二次函数在同一平面直角坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、 10. 反比例函数是常数,且与二次函数在同一坐标系内的大致图象是( )A、
10. 反比例函数是常数,且与二次函数在同一坐标系内的大致图象是( )A、 B、
B、
C、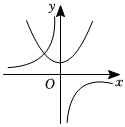 D、
D、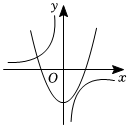
三、一次函数、反比例函数、二次函数图象共存
-
11. 已知反比例函数的图象如图所示,则二次函数和一次函数在同一平面直角坐标系中的图象可能是
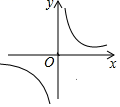 A、
A、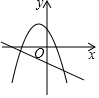 B、
B、 C、
C、 D、
D、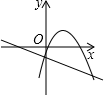 12. 二次函数的图象如图所示,则一次函数与反比例函数的图象可能是( )
12. 二次函数的图象如图所示,则一次函数与反比例函数的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 13. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
13. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )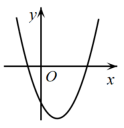 A、
A、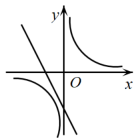 B、
B、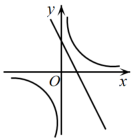 C、
C、 D、
D、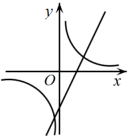 14. 已知反比例函数y=在第一象限内的图象与一次函数y=-x+b的图象如图所示,则函数的图象可能为( )
14. 已知反比例函数y=在第一象限内的图象与一次函数y=-x+b的图象如图所示,则函数的图象可能为( ) A、
A、 B、
B、 C、
C、 D、
D、 15. 一次函数 , 二次函数 , 反比例函数在同一直角坐标系中图象如图所示,则n的取值范围是( )
15. 一次函数 , 二次函数 , 反比例函数在同一直角坐标系中图象如图所示,则n的取值范围是( ) A、 B、 C、 D、16. 王老师在上函数复习课时,利用列表法给出了变量x,y的三组对应值如下表,你觉得这三点可以同时位于( )的图象上.
A、 B、 C、 D、16. 王老师在上函数复习课时,利用列表法给出了变量x,y的三组对应值如下表,你觉得这三点可以同时位于( )的图象上.x
……
1
2
4
……
y
……
……
A、一次函数和反比例函数 B、二次函数和反比例函数 C、一次函数和二次函数 D、一次函数和二次函数和反比例函数四、两个不同的二次函数图象与性质综合
-
17. 若二次函数y=x2+与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )A、这两个函数图象有相同的对称轴 B、这两个函数图象的开口方向相反 C、方程-x2+k=0没有实数根 D、二次函数y=-x2+k的最大值为18. 两个不同的二次函数与的图象有相同的对称轴,则下列结论不正确的是( )A、这两个函数图象的开口方向相反 B、这两个函数图象的都经过点 C、这两个函数图象的关于轴对称 D、二次函数的最大值为19. 甲、乙两个二次函数分别为y=(x+20)2+60、y=﹣(x﹣30)2+60,判断下列叙述何者正确?( )A、甲有最大值,且其值为x=20时的y值 B、甲有最小值,且其值为x=20时的y值 C、乙有最大值,且其值为x=30时的y值 D、乙有最小值,且其值为x=30时的y值20. 已知二次函数为常数图象上两个不同的点 , , 且有以下四个结论:该二次函数图象与轴一定有两个不同的交点;若一次函数经过点 , , 则当时,总有;当时,;当时,;以上结论中正确的是( )A、 B、 C、 D、21. 如图,两个二次函数的图象,其顶点P , Q都在x轴上,且有一水平线与两图象相交于A , B , C , D四点,若 , 则的长度为 .
 22. 定义:若两个二次函数的图象关于轴对称,则称互为“对称二次函数”.(1)、已知二次函数 , 则它的“对称二次函数”的顶点坐标为.(2)、已知关于的二次函数和 , 其中的图象经过点.若与互为“对称二次函数”,求函数的表达式;(3)、在(2)的条件下,当时,的最小值为-2,请直接写出的值.23. 如图,某课外小组利用几何画板来研究二次函数的图象,给出二次函数解析式(b , c为常数),通过输入不同的b、c的值,在几何画板的展示区得到对应的抛物线.若所得抛物线恰好经过和两点,解决下列问题.
22. 定义:若两个二次函数的图象关于轴对称,则称互为“对称二次函数”.(1)、已知二次函数 , 则它的“对称二次函数”的顶点坐标为.(2)、已知关于的二次函数和 , 其中的图象经过点.若与互为“对称二次函数”,求函数的表达式;(3)、在(2)的条件下,当时,的最小值为-2,请直接写出的值.23. 如图,某课外小组利用几何画板来研究二次函数的图象,给出二次函数解析式(b , c为常数),通过输入不同的b、c的值,在几何画板的展示区得到对应的抛物线.若所得抛物线恰好经过和两点,解决下列问题. (1)、求与抛物线相对应的b、c的值;(2)、若把抛物线相对应的b、c的值交换后,再次输入得到新的抛物线 , 求抛物线与x轴交点的坐标,并说明抛物线是否经过的顶点;(3)、另有直线l:与抛物线交于点P , Q , 与抛物线交于点M , N , 若的值是整数,请直接写出n的最大值.24. 定义:两个二次项系数之和为 , 对称轴相同,且图像与y轴交点也相同的二次函数互为友好同轴二次函数.例如:的友好同轴二次函数为.(1)、函数的友好同轴二次函数为.(2)、当时,函数的友好同轴二次函数有最大值为 , 求的值.(3)、已知点分别在二次函数及其友好同轴二次函数的图像上,比较的大小,并说明理由.25. 阅读以下材料,并解决相应问题:
(1)、求与抛物线相对应的b、c的值;(2)、若把抛物线相对应的b、c的值交换后,再次输入得到新的抛物线 , 求抛物线与x轴交点的坐标,并说明抛物线是否经过的顶点;(3)、另有直线l:与抛物线交于点P , Q , 与抛物线交于点M , N , 若的值是整数,请直接写出n的最大值.24. 定义:两个二次项系数之和为 , 对称轴相同,且图像与y轴交点也相同的二次函数互为友好同轴二次函数.例如:的友好同轴二次函数为.(1)、函数的友好同轴二次函数为.(2)、当时,函数的友好同轴二次函数有最大值为 , 求的值.(3)、已知点分别在二次函数及其友好同轴二次函数的图像上,比较的大小,并说明理由.25. 阅读以下材料,并解决相应问题:小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1、b1、c1是常数)与y=a2x2+b2x+c2(a2≠0,a2、b2、c2是常数)满足a1+a2=0,b1=b2 , c1+c2=0,则这两个函数互为“旋转函数”.求函数y=2x2﹣3x+1的旋转函数,小明是这样思考的,由函数y=2x2﹣3x+1可知,a1=2,b1=﹣3,c1=1,根据a1+a2=0,b1=b2 , c1+c2=0,求出a2 , b2 , c2就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)、写出函数y=x2﹣4x+3的旋转函数.(2)、若函数y=5x2+(m﹣1)x+n与y=﹣5x2﹣nx﹣3互为旋转函数,求(m+n)2020的值.(3)、已知函数y=2(x﹣1)(x+3)的图象与x轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1 , 试求证:经过点A1、B1、C1的二次函数与y=2(x﹣1)(x+3)互为“旋转函数”.