二次函数图象与性质—浙教版数学九（上）知识点训练

试卷更新日期：2024-11-23 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 下列二次函数的图象中，顶点在第二象限的是（）

A、 $y = {(x - 1)}^{2} + 3$ B、 $y = {(x - 1)}^{2} - 3$ C、 $y = {(x + 1)}^{2} + 3$ D、 $y = {(x + 1)}^{2} - 3$

查看试题解析
2. 二次函数y= $x^{2}$ 的图象向右平移3个单位，向下平移2个单位，得到新的图象的函数表达式是（）

A、 $y = {(x + 3)}^{2} + 2$ B、 $y = {(x - 3)}^{2} + 2$ C、 $y = {(x + 3)}^{2} - 2$ D、 $y = {(x - 3)}^{2} - 2$

查看试题解析
3. 已知点（2，y₁），（1，y₂），（－1，y₃）在抛物线y＝－x²＋2x＋m上，则（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} > y_{1} > y_{3}$ D、 $y_{2} > y_{3} > y_{1}$

查看试题解析
4. 二次函数y＝ax²＋bx＋c的图象如图所示，则点（a，b＋c）位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 对于抛物线y＝3（x+2）²﹣1，下列判断不正确的是（）

A、抛物线的顶点坐标为（﹣2，﹣1） B、把抛物线向右平移1个单位，再向上平移2个单位，得到抛物线y＝3（x+1）²+1 C、当x＞﹣2时，y随x的增大而增大 D、若点A（2，y₁），B（﹣3，y₂）在抛物上，则y₁＜y₂

查看试题解析
6. 若－1≤x≤m时，函数y＝(x－2)²＋1的最大值为17，则m＝．

查看试题解析
7. 已知二次函数 $y = x^{2} - 4 x + c$ 的图象经过点 $P (- 1, y_{1})$ 和 $Q (m, y_{2})$ ．若 $y_{1} < y_{2}$ ，则m的取值范围是．

查看试题解析
8. 已知二次函数经过点 $(- 1 ， 0)$ ， $(3 ， 0)$ ，且最大值为 $4$ ．

(1)、求二次函数的解析式；

(2)、在平面直角坐标系 $x O y$ 中，画出二次函数的图象；

(3)、当 $1 < x < 4$ 时，结合函数图象，直接写出 $y$ 的取值范围．

查看试题解析
9. 已知二次函数的解析式为 $y = a x^{2} + (a + 1) x + b$ ，其中 $a - b = 4$ .

(1)、若点 $^{(1, 3)}$ 在该函数图象上，求这个二次函数的解析式.

(2)、若 $(x_{1}, y_{1}) 、 (x_{2}, y_{2})$ 是二次函数图象上两个不同的点；当 $x_{1} + x_{2} = 2$ 时， $y_{1} = y_{2}$ ，求 $a$ 的值.

(3)、若该二次函数图象过点 $(- 1, t)$ ，且当 $x \geq - 1$ 时 $y$ 随 $x$ 的增大而增大，求 $t$ 的取值范围.

查看试题解析
10. 已知抛物线 $y = x^{2} + b x + c$ 与x轴交于点 $(- 3, 0)$ 与 $(5, 0)$ ．

(1)、求该抛物线的解析式及它的对称轴．

(2)、点 $(1, m)$ 在该抛物线上，求m的值．

(3)、当函数值 $y > 0$ 时，请直接写出自变量x的取值范围______．

(4)、当 $- 3 < x < 2$ 时，请直接写出函数y的取值范围______．

查看试题解析

二、能力提升

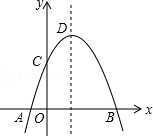
11. 如图，抛物线y＝﹣x²+2x+m+1交x轴于点A（a ， 0）和B（b ， 0），交y轴于点C ，抛物线的顶点为D ，下列四个命题：①当x＞0时，y＞0； ②若a＝﹣1，则b＝4；
③抛物线上有两点P（x₁ ， y₁）和Q（x₂ ， y₂），若x₁＜1＜x₂ ，且x₁+x₂＞2，则y₁＞y₂；
④点C关于抛物线对称轴的对称点为E ，点G ， F分别在x轴和y轴上，当m＝2时，四边形EDFG周长的最小值为 $6 \sqrt{2}$ ．其中真命题的序号是（）

A、① B、② C、③ D、④

查看试题解析
12. 设函数 $y_{1} = {(x - a_{1})}^{2}$ ， $y_{2} = {(x - a_{2})}^{2}$ ， $y_{3} = {(x - a_{3})}^{2}$ ．直线x＝b的图象与函数y₁ ， y₂ ， y₃的图象分别交于点A（b ， c₁），B（b ， c₂），C（b ， c₃），（）

A、若b＜a₁＜a₂＜a₃ ，则c₂＜c₃＜c₁ B、若a₁＜b＜a₂＜a₃ ，则c₁＜c₂＜c₃ C、若a₁＜a₂＜b＜a₃ ，则c₃＜c₂＜c₁ D、若a₁＜a₂＜a₃＜b ，则c₃＜c₂＜c₁

查看试题解析
13. 已知二次函数 $y = a x_{}^{2} + b x + 2$ （ $a \neq 0$ ），经过点P（ $m$ ， 12）．当 $y \leq - 1$ 时， $x$ 的取值范围为 $t - 1 \leq x \leq - 3 - t$ ．则如下四个值中有可能为 $m$ 的是（）

A、2 B、3 C、4 D、5

查看试题解析
14. 二次函数 $y = a x^{2} + b x + c （ a$ 、 $b$ 、 $c$ 是常数，且 $a \neq 0 ）$ 的自变量 $x$ 与函数值 $y$ 的部分对应值如下表：
x
…
-1
0
1
2
…
y … m 2 2 n …
且当 $x = \frac{3}{2}$ 时，对应的函数值 $y < 0 .$ 有以下结论： $① a b c > 0$ ； $② m + n < - \frac{20}{3}$ ； $③$ 关于 $x$ 的方程 $a x^{2} + b x + c = 0$ 的负实数根在 $- \frac{1}{2}$ 和 $0$ 之间； $④ P_{1} （ t - 1 ， y_{1} ）$ 和 $P_{2} （ t + 1 ， y_{2} ）$ 在该二次函数的图象上，则当实数 $t > \frac{1}{3}$ 时， $y_{1} > y_{2}$ ．
其中正确的结论是（）

A、 $① ②$ B、 $③ ④$ C、 $② ③ ④$ D、 $② ③$

查看试题解析
15. 若抛物线和两坐标轴的交点分别为(0，2)，(m，0)，(m+6，0)，当0<x< $\frac{1}{2}$ m+2时，总有y>2，则m的取值范围是．

查看试题解析
16. 在平面直角坐标系中， $O$ 为坐标原点，抛物线 $y = a x^{2} - 4 a x - 3$ 与 $y$ 轴交于点 $A$ ，过点 $A$ 作 $x$ 轴的平行线交抛物线于点 $B$ ，抛物线顶点为 $P$ ．若直线 $O P$ 交直线 $A B$ 于点 $C$ ，且 $4 B C = 3 A B$ ，则 $a$ 的值为．

查看试题解析
17. 已知二次函数y＝ax2＋bx＋3（a≠0，b是实数）图象经过四点：（－1，m），（1，n），（2，3），（4，p）．

(1)、若m＝4，①求二次函数的表达式；②已知x≤2k－3时，y随x的增大而减小，求k的最大值．

(2)、若m，n，p这三个实数中，有且只有一个是负数，求a的取值范围．

查看试题解析
18.

(1)、【问题初探】
综合与实践数学活动课上，张老师给出了一个问题：
已知二次函数y＝x²+2x－3，当－2≤x≤2时，y的取值范围为；
①小伟同学经过分析后，将原二次函数配方成y＝a(x－h)²+k
形式，确定抛物线对称轴为直线x＝h ，通过－2、h和2的大小
关系，分别确定了最大值和最小值，进而求出y的取值范围；
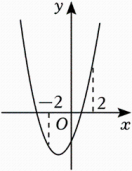
②小军同学画出如图的函数图象，通过观察图象确定了y的取值范围；请你根据上述两名同学的分析写出y的取值范围是；

(2)、【类比分析】
张老师发现两名同学分别从“数”和“形”的角度分析、解决问题，为了让同学们更好感悟“数形结合”思想，张老师将前面问题变式为下面问题，请你解答：已知二次函数y＝－x²+2x－3，当－2≤x≤2时，求y的取值范围；

(3)、【学以致用】
已知二次函数y＝－x²+6x－5，当a≤x≤a+3时，二次函数的最大值为y₁ ，最小值为y₂ ，若y₁－y₂＝3，求a的值．

查看试题解析

三、拓展创新

19. 如图，已知在平面直角坐标系xOy中，一段抛物线. $y = - x^{2} + 6 x (0 \leq x \leq 6),$ 记为抛物线C₁ ，它与x轴交于点O，A₁；将抛物线C₁绕点A₁旋转180°得抛物线C₂ ，交x轴于点A₁ ， A₂；将抛物线C₂绕点A₂ ，旋转180°得抛物线C₃ ，交x轴于点A₂ ， A₃；……如此进行下去，得到一条“波浪线”，若点M(2023，m)在此“波浪线”上，则m的值为（）

A、-9 B、-5 C、9 D、5

查看试题解析
20. 在平面直角坐标系xOy中，我们称横坐标、纵坐标都为整数的点为“整点”．抛物线y＝ax²－2ax＋2a（a为常数）与直线y＝x交于M、N两点，若线段MN与抛物线围成的区域（含边界）内恰有4个“整点”，则a的取值范围是．

查看试题解析
21. 【定义】在平面直角坐标系中，对“纵横值”给出如下定义：点 $A (x, y)$ 是函数图象上任意一点，纵坐标y与横坐标x的差“ $y - x$ ”称为点A的“纵横值”．函数图象上所有点的“纵横值”中的最大值称为函数的“最优纵横值”．
【举例】已知点 $A (1, 3)$ 在函数 $y = 2 x + 1$ 图象上．点 $A (1, 3)$ 的“纵横值”为 $y - x = 3 - 1 = 2$ ；函数 $y = 2 x + 1$ 图象上所有点的“纵横值”可以表示为 $y - x = 2 x + 1 - x = x + 1$ ，当 $3 \leq x \leq 6$ 时， $x + 1$ 的最大值为 $6 + 1 = 7$ ，所以函数 $y = 2 x + 1 (3 \leq x \leq 6)$ 的“最优纵横值”为7．
【问题】根据定义，解答下列问题：

(1)、①点 $B (- 6, 2)$ 的“纵横值”为；
②求出函数 $y = \frac{4}{x} + x (2 \leq x \leq 4)$ 的“最优纵横值”；

(2)、若二次函数 $y = - x^{2} + b x + c$ 的顶点在直线 $x = \frac{3}{2}$ 上，且最优纵横值为5，求c的值；

(3)、若二次函数 $y = - x^{2} + (2 b + 1) x - b^{2} + 3$ ，当 $- 1 \leq x \leq 4$ 时，二次函数的最优纵横值为2，直接写出b的值．

查看试题解析

x	…	-1	0	1	2	…
y	…	m	2	2	n	…