广东省深圳市南山区2024-2025学年七年级上学期期中考试数学试卷

试卷更新日期：2024-11-20 类型：期中考试

进入出卷网下载

一、选择题（每小题3分）

1. 中国是最早采用正负数来表示相反意义的量的国家，如果盈利 $60$ 元，记作“ $+ 60$ 元”，那么亏损 $20$ 元，记作（）

A、 $- 20$ 元 B、 $+ 20$ 元 C、 $- 40$ 元 D、 $+ 40$ 元

查看试题解析
2. 据统计，2024年端午节假期，福建省各地推出多项文旅活动，全省累计共接待游客 $680.41$ 万人次，实现旅游收入 $48.37$ 亿元．将数据 $4837000000$ 用科学记数法表示为（）

A、 $4.837 \times 10^{8}$ B、 $48.37 \times 10^{8}$ C、 $4.837 \times 10^{9}$ D、 $0.4837 \times 10^{10}$

查看试题解析
3. 下列各组数中，互为相反数的是（）

A、 $|+ 2|$ 与 $|- 2|$ B、 $- |+ 2|$ 与 $+ (- 2)$ C、 $- (- 2)$ 与 $+ (+ 2)$ D、 $- (- 3)$ 与 $- |- 3|$

查看试题解析
4. 下列几何体中可以由平面图形绕某条直线旋转一周得到的是（）

A、 B、 C、 D、

查看试题解析
5. 如果单项式 $- 3 x^{n} y$ 与 $3 x^{2} y^{m}$ 是同类项，那么 $m + n =$ （）

A、0 B、1 C、2 D、3

查看试题解析
6. 如图是一个计算机的运算程序，若一开始输入的x值为 $- \frac{1}{2}$ ，则输出的结果y是（）．

A、 $- 14$ B、 $- 17$ C、 $- 12$ D、1

查看试题解析
7. 已知 $3 x^{3} + x$ 的值是 $- 2$ ，则 $- 6 x^{3} - 2 x + 5$ 的值为（）

A、 $- 9$ B、9 C、7 D、3

查看试题解析
8. 已知整数 $a_{0}$ ， $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， ……，满足下列条件： $a_{0} = 0$ ， $a_{1} = - | a_{0} + 1 |$ ， $a_{2} = - | a_{1} + 2 |$ ， $a_{3} = - | a_{2} + 3 |$ ， ……，以此类推， $a_{2023}$ 的值为（）．

A、 $- 1011$ B、 $- 1012$ C、 $- 1013$ D、 $- 2023$

查看试题解析

二、填空题（每小题3分）

9. 比较大小： $- 8$ $- 9$ ， $- | - \frac{7}{8} |$ $- (+ \frac{5}{6})$ ， $(- 3)^{5}$ $- 3^{5}$ （填“＜”、“＝”或“＞”）．

查看试题解析
10. 单项式 $- \frac{1}{2} x^{2} y$ 的系数与次数分别是和．

查看试题解析
11. 如果 $| x - 2 | + | y + 3 | = 0$ ，则 $x + y =$ ．

查看试题解析
12. 若“⊙”表示一种新运算，规定 $a ⊙ b = a \times b - a$ ，则 $(- 1) ⊙ (- 5) =$ ．

查看试题解析
13. 若有理数a ， b ， c在数轴上的位置如图所示，则 $| a - c | - | b + c |$ 可化简为．

查看试题解析

三、解答题（共7小题）

14. 计算：

(1)、 $23 - 17 - (- 7) + (- 16)$ ；

(2)、 $(- 0.5) + 3 \frac{1}{4} + 2.75 + (- 5 \frac{1}{2})$ ；

(3)、 $\frac{4}{21} \div | - 2 | \times (- 4 \frac{1}{5})$ ；

(4)、 $- 2^{3} \div \frac{4}{9} \times {(- \frac{2}{3})}^{2} - | - 2 |$ ；

(5)、 $(\frac{5}{6} - \frac{3}{4} + \frac{1}{3}) \div (- \frac{1}{12})$ ；

(6)、 $99 \frac{24}{25} \times (- 5)$ ．

查看试题解析
15.

(1)、先化简再求值： $2 (x^{2} y + x y) - 3 (x^{2} y - x y) - 4 x^{2} y$ ，其中 $x = 1$ ， $y = - 1$ ．

(2)、已知 $A = - 3 x^{2} - 2 m x + 3 x + 1$ ， $B = 2 x^{2} + 2 m x - 1$ ．若 $2 A + 3 B$ 的值与x的取值无关，求m的值．

查看试题解析
16. 把下列各数表示在数轴上，然后把这些数按从小到大的顺序用“ $<$ ”连接起来．
$- 1^{2}$ ， $- |- 3|$ ， 0， $- (- 1.5)$ ， ${(- 2)}^{2}$

查看试题解析
17. 如图是由棱长都为1cm的6块小正方体组成的简单几何体.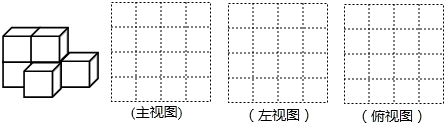

(1)、请在方格中画出该几何体的三个视图.

(2)、如果在这个几何体上再添加一些小正方体，并保持主视图和左视图不变，最多可以再添加块小正方体.

查看试题解析
18. 已知：a、b互为倒数，c、d互为相反数， $|m| = 2$ ， n是绝对值最小的数，求代数式 $3 a b - 2024 (c + d) + n + m^{2}$ 的值．

查看试题解析
19. 最近几年时间，我国的新能源汽车产销量大幅增加，小明家新换了一辆新能源纯电汽车，他连续7天记录了每天行驶的路程（如表），以50km为标准，多于50km的记为“＋”，不足50km的记为“-”，刚好50km的记为“0”．

第一天
第二天
第三天
第四天
第五天
第六天
第七天
里程（km）
$- 8$
$- 10$
$- 14$
0
$+ 24$
$+ 31$
$+ 35$

(1)、这7天里路程最多的一天比最少的一天多走km．

(2)、请求出小明家的新能源汽车这七天一共行驶了多少千米？

(3)、已知新能源汽车每行驶100km耗电量为15度，每度电为0.4元，请计算小明家这7天的行驶费用是多少钱？

查看试题解析
20. 观察下面的变化规律，解答下列问题：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ， $\frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$ ．

(1)、若n为正整数，猜想 $\frac{1}{n (n + 1)} =$ ___；

(2)、计算： $\frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} + \dots + \frac{1}{99 \times 100}$ ；

(3)、计算： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \frac{1}{7 \times 9} + \frac{1}{9 \times 11} + \frac{1}{11 \times 13} + \frac{1}{13 \times 15}$ ．

查看试题解析

	第一天	第二天	第三天	第四天	第五天	第六天	第七天
里程（km）	$- 8$	$- 10$	$- 14$	0	$+ 24$	$+ 31$	$+ 35$