广东省深圳市深圳高级中学2024-2025学年七年级上学期期中考试数学试卷

试卷更新日期：2024-11-20 类型：期中考试

进入出卷网下载

一、单选题：（每小题3分，共24分）

1. 中国古代著作《九章算术》在世界数学史上首次正式引入负数．如果盈利90元记作 $+$ 90元，那么亏本70元记作（）

A、 $-$ 60元 B、 $-$ 70元 C、 $+$ 60元 D、 $\pm$ 70元

查看试题解析
2. 为庆祝中华人民共和国成立75周年，10月1日、2日两天深圳举行舰艇开放日活动，市民可以在南山区蛇口邮轮母港参观“国庆回家”的深圳舰，深圳舰被称为“神州第一舰”，该舰经现代化改进后满载排水量达6600吨．数据6600用科学记数法可表示为（）

A、66×10² B、6.6×10³ C、6.6×10⁴ D、0.66×10⁵

查看试题解析
3. 下列比较大小正确的是（）

A、 $(- 3)^{3} > (- 2)^{3}$ B、 $(- 2)^{3} > (- 2)^{2}$ C、 $- \frac{2}{3} < - \frac{3}{2}$ D、 $- (- 3) > - | - 3 |$

查看试题解析
4. 如图，用一个平面从不同的位置，沿着不同的方向取截一个圆柱，圆柱的截面不可能是（）

A、 B、 C、 D、

查看试题解析
5. 如果 $a - 3 b = - 2$ ，那么代数式 $7 - a + 3 b$ 的值是（）

A、0 B、5 C、7 D、9

查看试题解析
6. 若规定 $a \otimes b = a \div b \times \frac{- 1}{b}$ ，则 $(- 9) \otimes \frac{1}{3}$ 的结果为（）

A、9 B、 $- 9$ C、81 D、 $- 81$

查看试题解析
7. 长方形窗户上的装饰物（遮光）如图中阴影部分所示，它是由两个半径均为b的四分之一圆组成，则该窗户能射进阳光部分的面积是（　　）

A、 $\frac{π}{2} b^{2}$ B、 $2 a b - π b^{2}$ C、 $2 a b - \frac{π}{2} b^{2}$ D、 $2 a b - \frac{π}{4} b^{2}$

查看试题解析
8. 下图是由同样大小的 $△$ 按一定规律排列而成，其中第①个图形中有4个 $△$ ，第②个图形中有9个 $△$ ，第③个图形中有14个 $△$ ， …，则第⑧个图形中 $△$ 的个数为（）

A、34 B、39 C、40 D、44

查看试题解析

二、填空题：（每小题3分，共15分）

9. 若a，b互为倒数，则 ${(- a b)}^{2024} =$ ．

查看试题解析
10. 若 $x^{m} y^{2}$ 与 $4 x^{3} y^{n}$ 是同类项，则 $m + n =$ ．

查看试题解析
11. 按照如图所示的平面展开图折叠成正方体后，相对面上的两个数都互为相反数，那么 $a + b =$ ．

查看试题解析
12. 数 $a, b, c$ 在数轴上对应的点的位置如图所示，则 $| a + c | - | a - b | + | b | =$ ．

查看试题解析
13. 如果记 $f (x) = \frac{x^{2}}{1 + x^{2}}$ ，即当 $x = 1$ 时， $f (1) = \frac{1^{2}}{1 + 1^{2}} = \frac{1}{2}$ ，那么
$f (1) + f (2) + f (\frac{1}{2}) + f (3) + f (\frac{1}{3}) + ⋯ + f (n) + f (\frac{1}{n}) =$ ．（结果用含 $n$ 的代数式表示， $n$ 为
正整数）

查看试题解析

三、解答题：（本大题共7小题，其中第14题8分，第15题7分，第16题8分，第17题7分，第18题8分，第19题11分，第20题12分，共61分）

14. 计算：

(1)、 $(\frac{5}{6} + \frac{2}{3} - \frac{3}{4}) \times (- 24)$

(2)、 $- 3^{2} - (- 1 \frac{1}{2}) \times \frac{4}{3} - 8 \div | - \frac{2}{3} |$

查看试题解析
15. 已知代数式 $M = (2 a^{2} + a b - 4) - 2 (2 a b + a^{2} + 1)$ ．

(1)、化简 $M$ ；

(2)、当 $a = 2$ ， $b = - 3$ 时，求 $M$ 的值．

查看试题解析
16. 某手工作坊计划一天生产50个布娃娃，但由于各种原因，实际每天生产布娃娃数量与计划每天生产布娃娃数量相比有出入．下表是某一周的生产情况（超过计划数量的部分记作正数，不足计划数量的部分记作负数，单位：个）：
星期
一
二
三
四
五
六
日
增减
$- 4$
$+ 5$
$+ 3$
$- 6$
$- 7$
$+ 12$
$- 2$

(1)、根据记录可知前四天共生产布娃娃个；

(2)、求该作坊本周实际生产布娃娃的个数；

(3)、该作坊实行每日计件工资制，每生产一个布娃娃可得20元，若超额完成任务，则超过部分每个另奖8元，若未能完成任务，则少生产一个扣5元，那么该作坊工人这一周的工资总额是多少元？

查看试题解析
17. 劳动技术课程是基础教育的重要课程之一，其根本使命是全面提高未来国民的基本劳动技术素养，培养具有技术知识、创新思维、实践能力的一代新人．我校将利用天台劳动基地展开一系列的劳动实践操作活动．如图所示，天台上有块长为20米，宽为10米的长方形空地，现在将其余三面留出宽都是 $x$ 米的小路，中间余下的长方形部分做菜地．

(1)、用含 $x$ 的式子表示菜地的周长；

(2)、当 $x = 1.2$ 米时，求菜地的周长．

查看试题解析
18. 归纳是发现数学结论、解决数学问题的一种重要策略．“归纳”的过程，即从几种特殊情形出发，进而找到一般规律的过程．在数学的学习过程中，我们经常用这样的策略探究规律．
【数学问题】平面图的顶点数、边数与区域数之间存在什么样的数量关系？
【问题探究】为了解决这个问题，我们可以从类似于（ $a$ ）、（ $b$ ）、（ $c$ ）、（ $d$ ）、（ $e$ ）五个图等具体的情形入手，借助表格探索平面图的顶点数 $x$ 、边数 $y$ 与区域数 $z$ 之间的一般规律．
图
顶点数 $x$
边数 $y$
区域数 $z$
$(a)$
3
3
1
$(b)$
4
6
3
$(c)$
6
9
4
$(d)$
8
$m$
5
$(e)$
10
15
$n$
【问题解决】

(1)、将表格数据补充完整， $m =$ ； $n =$ ；

(2)、猜想：一个平面图的顶点数 $x$ 、边数 $y$ 、区域数 $z$ 之间的数量关系为：；

(3)、现已知某一平面图有999个顶点和999个区域，试根据（2）中猜想的关系，确定这个图有多少条边？

查看试题解析
19. 规定： $A, B, C$ 是数轴上的三个点，点 $C$ 将线段 $A B$ 分成 $A C$ 和 $B C$ 两部分，若 $B C = 2 A C$ 或 $A C = 2 B C$ ，则称线段 $A C, B C$ 互为二倍伴侣线段．点 $A$ 表示的数为 $a$ ，点 $B$ 所表示的数为 $b$ 且 $a, b$ 满足 $(a + 3)^{2} +$ $| b - 5 | = 0$ ．

(1)、 $a =$ ， $b =$ ；

(2)、若点 $C$ 在线段 $A B$ 上，且线段 $A C, B C$ 互为二倍伴侣线段，则点 $C$ 表示的数为；

(3)、点 $M$ 从点 $A$ 出发，同时点 $N$ 从点 $B$ 出发，沿数轴分别以每秒3个单位长度和每秒1个单位长度的速度向右运动，设运动时间为 $t$ 秒，当线段 $M B, N B$ 互为二倍伴侣线段时，求 $t$ 的值．

查看试题解析

20. 七（1）班数学项目小组为解决小琴奶奶家储物问题，计划将闲置纸板箱制作成储物盒．

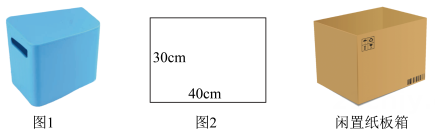
素材1	如图1，图中是小琴奶奶家需要设置储物盒的区域，该区域可以近似看成一个长方体，底面尺寸如图2所示．
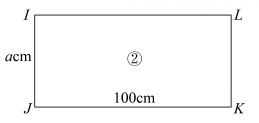
素材2	如图是利用闲置纸板箱侧面拆解出的①，②两种宽均为 $a$ cm（ $a < 50$ cm）长方形纸板，纸板的厚度忽略不计．
	长方形纸板①	长方形纸板②

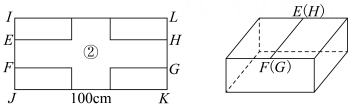
	分别将长方形纸板①和②以不同的方式制作储物盒．
	长方形纸板①的制作方式	长方形纸板②制作方式
	裁去角上4个相同的小正方形，折成一个无盖长方体储物盒．	将纸片四个角裁去4个相同的小长方形，折成一个有盖的长方体储物盒．
目标1	熟悉材料	按照长方形纸板①的制作方式制成的储物盒能够无缝隙的放入储物区域，则长方形纸板宽 $a$ 为 ▲ cm．
目标2	利用目标1计算所得的数据 $a$ ，进行进一步探究．
	初步应用	⑴按照长方形纸板①的制作方式，为了更方便地放入或取出储物盒，盒子四周需要留出1cm宽度，求储物盒的容积．
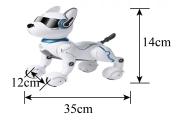
	储物收纳	⑵按照长方形纸板②的制作方式制作储物盒，若 $E F$ 和 $H G$ 两边恰好重合且无重叠部分，如图，是小琴奶奶家里一个玩具机械狗的实物图和尺寸大小，请设计一个各个面均不大于600cm²的储物盒收纳这只玩具狗．

查看试题解析

星期	一	二	三	四	五	六	日
增减	$- 4$	$+ 5$	$+ 3$	$- 6$	$- 7$	$+ 12$	$- 2$

图	顶点数 $x$	边数 $y$	区域数 $z$
$(a)$	3	3	1
$(b)$	4	6	3
$(c)$	6	9	4
$(d)$	8	$m$	5
$(e)$	10	15	$n$