浙江省杭州市十三中集团2024-2025学年九年级上学期数学期中试题卷

试卷更新日期：2024-11-18 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分，每小题给出的四个选项中，只有一个正确选项）

1. 下列事件是必然事件的是（）

A、明天早上会下雨 B、掷一枚硬币，正面朝上 C、任意一个三角形，它的内角和等于180° D、一个图形旋转后所得的图形与原图形不全等

查看试题解析
2. 在 $⊙ O$ 所在平面内有一点 $P$ ，若 $O P = 6, ⊙ O$ 半径为5，则点 $P$ 与 $⊙ O$ 的位置关系是（）

A、点 $P$ 在 $⊙ O$ 内 B、点 $P$ 在 $⊙ O$ 外 C、点 $P$ 在 $⊙ O$ 上 D、无法判断

查看试题解析
3. 从甲、乙、丙三人中任选一人参加青年志愿者活动，甲被选中的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 如图， $△ O A B$ 绕点 $O$ 顺时针旋转 $8 0^{°}$ 到 $△ O C D$ 的位置，已知 $∠ A O B = 4 5^{°}$ ，则 $∠ B O C$ 等于（）

A、55° B、45 C、40° D、35

查看试题解析
5. 二次函数y=（x-3）（x+5）的图象的对称轴是（）

A、直线x=3 B、直线x=-5 C、直线x=1 D、直线x=-1

查看试题解析
6. 如图，四边形BCD内接于⊙O，如果它的一个外角∠DCE=64，那么∠BOD=（）

A、 $12 8^{°}$ B、 $10 0^{°}$ C、 $12 0^{°}$ D、 $13 2^{°}$

查看试题解析
7. 二次函数 $y = m x^{2} + m x (m < 0)$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 某项目化研究小组只用一张矩形纸条和刻度尺，来测量一次性纸杯杯底的直径，小敏同学想到了如下方法：如图，将纸条拉直并紧贴杯底：纸条的上下边沿分别与杯底相交于A、B、C、D四点，然后利用刻度尺量得该纸条的宽为3.5cm，AB=4cm，CD=3cm.则该纸杯杯底的直径为（）

A、4.8cm B、5cm C、5.2cm D、6cm

查看试题解析
9. 已知函数y=ax²+2ax-1（a是常数，a≠0），下列结论正确的是（）

A、当a=1时，函数图象过点（-1，1） B、函数图象与x轴必有两个交点 C、不论a取何值，函数图象都经过点（-2，-1） D、若a<0，则当x≤-1时，y随x的增大而减小

查看试题解析
10. 已知⊙O为ΔABC的外接圆，AB=BC.过A作CO的垂线交CO延长线于点D，则下列选项一定成立的是（）

A、 $∠ B C A = ∠ D C A$ B、 $∠ D A C = 2 ∠ B A C$ C、 $A B > 2 A D$ D、 $4 A B^{2} < A D^{2} + C D^{2}$

查看试题解析

二、填空题（每小题3分，共18分）

11. 如表是某种植物的种子在相同条件下发芽率试验的结果.
种子个数
100
400
900
1500
2500
4000
发芽种子个数
92
352
818
1336
2251
3601
发芽种子频率
0.92
0.88
0.91
0.89
0.90
0.90
根据表中的数据，可估计该植物的种子发芽的概率为.

查看试题解析
12. 如图在平面直角坐标系中，过格点A，B，C作一圆弧，圆心坐标是．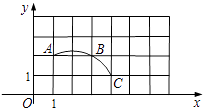

查看试题解析
13. 一只盒子中有红球m个，白球8个，黑球n个，每个球除颜色外都相同，从中任取一个球，取得白球的概率与不是白球的概率相同，那么m与n的和是

查看试题解析
14. 已知二次函数 $y = x^{2} - 2 x - 3$ ，当 $0 \leq x \leq 3$ 时， $y$ 的取值范围是.

查看试题解析
15. 如图，四边形ABCD内接于 $⊙ O$ ，对角线BD是 $⊙ O$ 的直径. $E$ 为 $⊙ O$ 内一点，满足 $A E ⊥ B C$ ， $C E ⊥ A B$ ，若 $B D = 4 \sqrt{3}, A E = 4$ ，则弦BC的长为.

查看试题解析
16. 二次函数 $y = a x^{2} + b x + c (a, b, c$ 是常数， $a \neq 0)$ 图象的对称轴是直线 $x = 1$ ，其图象一部分如图所示，对于下列说法：① $a b c < 0$ ；② $2 c > 3 b$ ；③方程 $a x^{2} + (b - \frac{1}{2}) x + c = 0$ 有两个不相等的实数根；④ $a \geq a m^{2} + b (m - 1)$ （ $m$ 为任意实数）.其中正确的是.（填写序号）

查看试题解析

三、解答题（本题有8小题，共72分,解答应写出文字说明，证明过程或推演步骤.）

17. 已知二次函数的图象顶点坐标是（0，0），且经过（1，-2）

(1)、求这个二次函数的表达式；

(2)、判断点P（-2，-8）是否在这条抛物线的图象上

查看试题解析
18. 如图，AB是 $⊙ O$ 的直径，点 $C$ 是 $⊙ O$ 上一点，连接 $B C, A C, O D ⊥ B C$ 于 $E$ ，交 $⊙ O$ 于点 $D$ .

(1)、求证：OD∥AC；

(2)、若BC=8，DE=2，求⊙O的半径，

查看试题解析
19. 作图题，根据要求作出以下图形：

(1)、在图1网格中直接画出△ABC绕点A逆时针旋转90°的图形；

(2)、在图2中，已知线段AB，尺规作图作出经过A，B两点的所有圆中最小的圆，（要求保留作图痕迹）

查看试题解析
20. 睡眠管理作为“五项管理”中的重要内容之一，也是学校教育重点关注的内容，某校为了解学生平均每天睡眠时间，随机抽取该校部分学生进行问卷调查，并将结果进行了统计和整理，绘制成如下统计表和不完整的统计图.
某校学生睡眠时间各类别人数情况统计图
学生类别
学生平均每天睡眠时间x（单位：小时）
A
7≤x<7.5
B
7.5≤x<8
C
8≤x<8.5
D
8.5≤x<9
E
x≥9

(1)、扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为.

(2)、请补全条形统计图.

(3)、被抽取调查的E类4名学生中有2名女生，2名男生，从这4人中随机抽取2人进行电话问访，请用画树状图或列表的方法，求恰好抽到2名男生的概率.

查看试题解析
21. 某商店购进一种商品，每件商品进价20元，规定该商品的售价不低于进价，且不高于进价的两倍.试销中发现这种商品每天的销售量，（件）与每件销售价x（元）的关系数据如下：
x
300
32
34
36
y
40
36
32
28

(1)、已知y与x满足一次函数关系，根据上表，求出了与x之间的关系式；

(2)、设该商店每天销售这种商品所获利润为w（元），求出每件商品销售价定为多少元时利润最大，并求出最大利润?

查看试题解析
22. 某地欲搭建一桥，桥的底部两端间的距离AB=L称跨度，桥面最高点到AB的距离CD=h称拱高，当L和h确定时，有两种设计方案可供选择：①抛物线型：②）圆弧型，已知这座桥的跨度L=20米，拱高h=5米.

(1)、如图1，若设计成抛物线型，以AB所在直线为x轴，B的垂直平分线为y轴建立坐标系，求此函数表达式；

(2)、如图2，若设计成圆弧型，求该圆弧所在圆的半径；

(3)、现有一艘宽为15米的货船，船舱顶部为方形，并高出水面2.2米，从以上两种方案中，任选一种方案，判断此货船能否顺利通过你所选方案的桥?并说明理由.

查看试题解析
23. 已知二次函数 $y = x^{2} - (2 m - 1) x + m^{2} - m$ （ $m$ 是常数，且 $m \neq 0$ ）

(1)、证明：不论 $m$ 取何值时，该二次函数图象总与 $x$ 轴有两个交点；

(2)、若 $A (n - 3, y_{1}), B (- n + 1, y_{2})$ 是该二次函数图象上的两个不同点，当 $y_{1} = y_{2}$ 时，求二次函数表达式；

(3)、若二次函数图象与 $x$ 轴两个交点的横坐标分别为 $x_{1}, x_{2}$ （其中 $x_{1} > x_{2}$ ）， $t$ 是关于 $m$ 的函数.且 $t = 1 - \frac{x_{2}}{x_{1}}$ ，当 $t < m$ 时，求 $m$ 的取值范围.

查看试题解析
24. 如图，在Rt $△ A B C$ 中， $∠ A C B = 9 0^{°}, B C$ 是 $⊙ O$ 的直径， $⊙ O$ 与边AB交于点D，E为BD的中点，连接CE，与AB交于点 $F$ .

(1)、若 $∠ A = 4 ∠ B$ ，求 $∠ E C B$ 的大小；

(2)、求证： $A C = A F$ ；

(3)、若 $B C = 6, \frac{E F}{F C} = \frac{1}{2}$ ，求 $△ A F C$ 的面积.

查看试题解析

种子个数	100	400	900	1500	2500	4000
发芽种子个数	92	352	818	1336	2251	3601
发芽种子频率	0.92	0.88	0.91	0.89	0.90	0.90

学生类别	学生平均每天睡眠时间x（单位：小时）
A	7≤x<7.5
B	7.5≤x<8
C	8≤x<8.5
D	8.5≤x<9
E	x≥9

x	300	32	34	36
y	40	36	32	28