广东省深圳市福田区红岭教育集团2024-2025学年八年级上学期数学期中试卷

试卷更新日期：2024-11-18 类型：期中考试

进入出卷网下载

一、选择题（共8小题，每小题3分，共24分）

1. 在直角坐标系中，点A（4，3）位于（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在﹣1.414，π， $\frac{22}{7}$ ， 3.142， $2 - \sqrt{3}$ ， 2.121121112…（相邻两个2之间1的个数逐次加1）中，无理数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列四组数为三角形的三边长，其中不能作为直角三角形三条边的是（　　）

A、6，8，10 B、3，4，5 C、5，12，13 D、1，2，3

查看试题解析
4. 下列计算中，正确的是（　　）

A、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $3 \sqrt{2} \times 2 \sqrt{3} = 6 \sqrt{5}$ D、 $\sqrt{24} \div \sqrt{6} = 2$

查看试题解析
5. 已知一次函数y＝kx+b（k≠0）的图象如图所示，则函数y＝kbx的图象一定经过（　　）

A、第一、三象限 B、第二、四象限 C、第一、二、三象限 D、第二、三、四象限

查看试题解析
6. 勾股定理是用代数思想解决几何问题最重要的工具，也是数形结合的纽带之一．如图，当秋千静止时，踏板B离地的垂直高度 $B E = 0.8 m$ ，将它往前推 $3 m$ 至C处时(即水平距离 $C D = 3 m$ )，踏板离地的垂直高度 $C F = 2.6 m$ ，它的绳索始终拉直，则绳索 $A C$ 的长是（）

A、 $3.4 m$ B、 $3.6 m$ C、 $3.8 m$ D、 $4.2 m$

查看试题解析
7. 已知直线y＝﹣3x+m过点A（﹣1，y₁）和点（﹣3，y₂），则y₁和y₂的大小关系是（）

A、y₁＞y₂ B、y₁＜y₂ C、y₁＝y₂ D、不能确定

查看试题解析
8. 甲、乙两人同起点同方向出发，匀速步行3000米，先到终点的人原地休息．已知甲先出发3分钟，甲、乙两人之间的距离y（米）与甲出发的时间t（分）之间的关系如图所示，则下列说法正确是（　　）

A、甲步行的平均速度为32米/分． B、乙步行的平均速度为20米/分． C、当t = 30时，乙到达终点． D、乙比甲提前4.5分钟到达终点．

查看试题解析

二、填空题（共5小题，每小题3分，共15分）

9. 16的算术平方根是

查看试题解析
10. P（﹣1，﹣2）关于y轴的对称点的坐标为．

查看试题解析
11. 如图，以原点O为圆心， $O B$ 为半径画弧与数轴交于点A，则点A在数轴上表示的数为.

查看试题解析
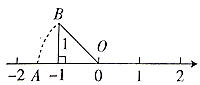12. 若y＝（k﹣3）x^|k^|﹣2+5是一次函数，则k＝．

查看试题解析
13. 如图所示，在△ABC中，AB：BC：AC＝3：4：5，且周长为36m，点P从点A开始沿AB边向B点以每秒1m的速度移动；点Q从点B沿BC边向点C以每秒2m的速度移动（Q运动到点C停止），如果同时出发，则过7秒时，点B到PQ的距离为．

查看试题解析

三、解答题（共7小题，其中14题12分，15题6分，16题8分，17题8分，18题10分，19题8分，20题9分，共61分）

14. 计算题

(1)、 $\frac{\sqrt{12} \times \sqrt{6}}{\sqrt{24}}$ ；

(2)、 $3 \sqrt{20} - \sqrt{45} - \sqrt{\frac{1}{5}}$ ；

(3)、 $\frac{\sqrt{27} + \sqrt{12}}{\sqrt{3}} - 1$ ；

(4)、 ${(\sqrt{3} - \sqrt{2})}^{2} + (\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})$ ．

查看试题解析
15. 已知 $\sqrt{a - 3} + \sqrt{3 - a} = 0$ ， 3b﹣4的立方根是2，c是 $\sqrt{6}$ 的整数部分．

(1)、求a、b、c的值；

(2)、求a+6b﹣c的平方根．

查看试题解析
16. 在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上（小正方形的顶点称为格点），请解答下列问题：

(1)、画出△ABC关于y轴对称的△A₁B₁C₁ ，点A₁与A、B₁与B对应，并写出点A₁的坐标 ▲ ；

(2)、已知点P是x轴上任意一点，则PB+PC的最小值是．

(3)、△ABC的面积是．

查看试题解析
17. 如图，已知直线l经过点A（0，1）与点B（2，3），且与x轴交于点C，点M是x轴上的一点．

(1)、求直线l的表达式及点C的坐标；

(2)、若△BCM的面积为3，求点M的坐标．

查看试题解析

18. 某校八年级开展了《为家人选择合适的手机资费套餐》项目学习．以下是小露同学帮奶奶选择手机资费套餐的活动报告，请你将其补充完整．

为家人选择合适的手机资费套餐活动报告

一、收集信息

收集并整理奶奶近六个月的话费账单，发现她使用流量和短信极少，故忽略流量和短信情况进行研究．根据她的月平均通话时间筛选出两款比较适合她的手机资费套餐．

甲套餐：月租费8元，送30分钟通话时间，超出的部分按每分钟0.25元计；

乙套餐：月租费29元，通话费按每分钟0.1元计．

二、建立模型

⑴．发现每月的手机资费y（元）与通话时间x（分）之间存在函数关系，y与x之间的关系式为：

$y_{甲} = {\begin{array}{l} 8 (8 \leq x \leq 30) \\ (___) \cdot (x > 30) \end{array}$ ， $y_{乙}$ ＝ ▲ （x≥0）．

⑵．为了直观比较，在同一坐标系内画出两个函数的图象（如图）．图中A点表示的实际意义是 ▲ ．

⑶．解决问题

根据图象可知：如果从节省费用的角度考虑，

当通话时间 ▲ 时，选择甲套餐更合适；

当通话时间 ▲ 时，选择乙套餐更合适．

查看试题解析

19. 如图，在一条东西走向河流的一侧有一村庄C，河边原有两个取水点A、B，其中 $A B = A C$ ，由于某种原因，由C到A的路现在已经不通，该村庄为方便村民取水，决定在河边新建一个取水点H（A、B、H在同一直线上），并新建一条路CH，测得 $C B = \sqrt{13}$ 千米， $C H = 3$ 千米， $H B = 2$ 千米．

(1)、CH是不是从村庄C到河边的最近路？请通过计算加以说明；

(2)、求新路CH比原路CA短多少千米？

查看试题解析
20. 如图，直线y $= - \frac{3}{2}$ x+b与x轴交于点A，与y轴交于点B，点P（2，3）在直线y $= - \frac{3}{2}$ x+b上，点C是线段OB上一点（不与点O，B重合）．

(1)、求点A，B的坐标．

(2)、连接PC，将△OPC沿直线PC翻折得到△DPC，点D为点O的对应点，点D在第一象限，且∠OCD＝90°．
①求点D的坐标．
②若直线y $= - \frac{3}{2}$ x+b与CD交于点E，在y轴上是否存在点Q，使△BEQ是以BE为腰的等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析