【基础版】北师大版数学九年级上册 4.5 相似三角形判定定理的证明 同步练习
试卷更新日期:2024-11-18 类型:同步测试
一、选择题
-
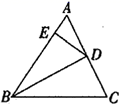
1. 如图,AD、BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( )
 A、AB∥CD B、 C、 D、2. 如图是老师画出的 , 已标出三边的长度,下面四位同学画出的三角形与老师画出的不一定相似的是( )
A、AB∥CD B、 C、 D、2. 如图是老师画出的 , 已标出三边的长度,下面四位同学画出的三角形与老师画出的不一定相似的是( ) A、
A、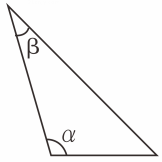 B、
B、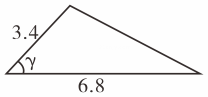 C、
C、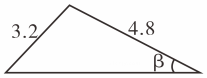 D、
D、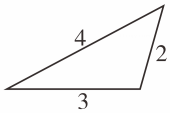 3. 下列图形,一定相似的是( )A、两个直角三角形 B、两个等腰三角形 C、两个等边三角形 D、两个菱形4. 下列各组条件中,能判定△ABC与△A'B'C'相似的是( )A、 B、 , 且∠A=∠C' C、 , 且∠B=∠A' D、 , 且∠B=∠B'5. △ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是( )A、AB=c,AC=b,BC=a,DE= , EF= , DF= B、AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1 C、AB=3,AC=4,BC=6,DE=12,EF=8,DF=6 D、AB= , AC= , BC= , DE= , EF=3,DF=36. 如图所示,是的边AC上一点,连结BP.下列条件中,不能判定的是( ).
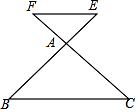
3. 下列图形,一定相似的是( )A、两个直角三角形 B、两个等腰三角形 C、两个等边三角形 D、两个菱形4. 下列各组条件中,能判定△ABC与△A'B'C'相似的是( )A、 B、 , 且∠A=∠C' C、 , 且∠B=∠A' D、 , 且∠B=∠B'5. △ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是( )A、AB=c,AC=b,BC=a,DE= , EF= , DF= B、AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1 C、AB=3,AC=4,BC=6,DE=12,EF=8,DF=6 D、AB= , AC= , BC= , DE= , EF=3,DF=36. 如图所示,是的边AC上一点,连结BP.下列条件中,不能判定的是( ). A、 B、 C、 D、7. 如图,在四边形ABCD中,已知∠ADC=∠BAC , 那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A、 B、 C、 D、7. 如图,在四边形ABCD中,已知∠ADC=∠BAC , 那么补充下列条件后不能判定△ADC和△BAC相似的是( ) A、CA平分∠BCD B、∠DAC=∠ABC C、AC2=BC•CD D、8. 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③ ,④ ,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )
A、CA平分∠BCD B、∠DAC=∠ABC C、AC2=BC•CD D、8. 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③ ,④ ,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )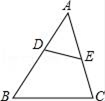 A、①②④ B、②④⑤ C、①②③④ D、①②③⑤
A、①②④ B、②④⑤ C、①②③④ D、①②③⑤二、填空题
-
9. 如图,线段AC、BD交于点O,请你添加一个条件: , 使△AOB∽△COD.
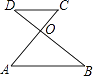 10. 如图,在△ABC中,D为边AC上的点,连接BD , 添加一个条件: , 可以使得△ADB∽△ABC . (只需写出一个)
10. 如图,在△ABC中,D为边AC上的点,连接BD , 添加一个条件: , 可以使得△ADB∽△ABC . (只需写出一个)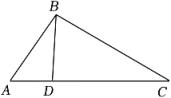 11. 如图,已知 , , , , 则 .
11. 如图,已知 , , , , 则 . 12. 如图,要使△ACD∽△ABC,只需添加条件(只要写出一种合适的条件即可).
12. 如图,要使△ACD∽△ABC,只需添加条件(只要写出一种合适的条件即可). 13. 如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D , 与AB及AC的延长线分别交于E , F , 写出图中的一对全等三角形是 ;一对相似三角形是 .
13. 如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D , 与AB及AC的延长线分别交于E , F , 写出图中的一对全等三角形是 ;一对相似三角形是 .
三、解答题
-
14. 如图,在中, , D是边上一点,.求证.
 15. 如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC·BE.
15. 如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC·BE.证明:△BCD∽△BDE.