【基础卷】第四章 相交线与平行线 单元测试 ——华师大版数学七年级上册
试卷更新日期:2024-11-17 类型:单元试卷
一、选择题:每题4分,共48分
-
1. 下列各图中,和是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,直线 , 相交于点O , , 若 , 则的度数为( )
2. 如图,直线 , 相交于点O , , 若 , 则的度数为( ) A、 B、 C、 D、3. 如图 , 生活中,有以下两个现象,对于这两个现象的解释,正确的是( )
A、 B、 C、 D、3. 如图 , 生活中,有以下两个现象,对于这两个现象的解释,正确的是( ) A、两个现象均可用两点之间线段最短来解释
A、两个现象均可用两点之间线段最短来解释
B、现象用垂线段最短来解释,现象用经过两点有且只有一条直线来解释
C、现象用垂线段最短来解释,现象用两点之间线段最短来解释
D、现象用经过两点有且只有一条直线来解释,现象用垂线段最短来解释4. 下列图形中,线段AD的长表示点A到直线BC距离的是( )A、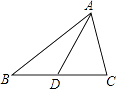 B、
B、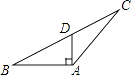 C、
C、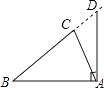 D、
D、 5. 如图,和是一对( )
5. 如图,和是一对( ) A、同位角 B、同旁内角 C、内错角 D、对顶角6. 英文字母中,存在同位角、内错角、同旁内角(不考虑字母宽度),下列字母中含同旁内角最多的是( )A、
A、同位角 B、同旁内角 C、内错角 D、对顶角6. 英文字母中,存在同位角、内错角、同旁内角(不考虑字母宽度),下列字母中含同旁内角最多的是( )A、 B、
B、 C、
C、 D、
D、 7. 有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③等角的补角相等;④在同一平面内,垂直于同一条直线的两条直线互相平行.其中真命题的个数为( )A、1 B、2 C、3 D、48. 下图给出了过直线外一点画已知直线的平行线的方法,其依据是( )
7. 有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③等角的补角相等;④在同一平面内,垂直于同一条直线的两条直线互相平行.其中真命题的个数为( )A、1 B、2 C、3 D、48. 下图给出了过直线外一点画已知直线的平行线的方法,其依据是( ) A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等9. 如图所示, , 则下列结论正确的是( )
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等9. 如图所示, , 则下列结论正确的是( ) A、 B、 C、 D、10. 如图所示,下列条件中能说明的是( )
A、 B、 C、 D、10. 如图所示,下列条件中能说明的是( ) A、 B、 C、 D、11. 如图,已知直线 , 平分 , , 则的度数是( )
A、 B、 C、 D、11. 如图,已知直线 , 平分 , , 则的度数是( ) A、 B、 C、 D、12. 某小区车库门口的曲臂道闸升降杜如图所示, 垂直地面 于 A 点, 平行于地面 , 若 ,则 的大小是( )
A、 B、 C、 D、12. 某小区车库门口的曲臂道闸升降杜如图所示, 垂直地面 于 A 点, 平行于地面 , 若 ,则 的大小是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:每题4分,共24分
-
13. 如图,直线相交于点O,已知 , 把分成两部分,且 , 则 .
 14. 如图,已知直线与直线相交于点 , , , 则
14. 如图,已知直线与直线相交于点 , , , 则 15. 已知直线EF及其外一点B,过B点作AB∥EF,过B点作BC∥EF,点A,C分别为直线AB,BC上任意一点,那么A,B,C三点一定在同一条直线上,依据是 .16. 如图,在三角形ABC中,F为AC延长线上一点,直线HG经过点B , 写出一个能判定的条件 . (写出一个即可)
15. 已知直线EF及其外一点B,过B点作AB∥EF,过B点作BC∥EF,点A,C分别为直线AB,BC上任意一点,那么A,B,C三点一定在同一条直线上,依据是 .16. 如图,在三角形ABC中,F为AC延长线上一点,直线HG经过点B , 写出一个能判定的条件 . (写出一个即可) 17. 光线从一种介质射向另一种介质时会发生折射如图,这是一块玻璃的 , 两面玻璃上下两个面的示意图,且 , 一束光从玻璃面的处射向玻璃面的处,但从玻璃面的处射出时发生了折射,使光线从变成了 , 为光线延长线上一点,已知 , , 则的度数为 .
17. 光线从一种介质射向另一种介质时会发生折射如图,这是一块玻璃的 , 两面玻璃上下两个面的示意图,且 , 一束光从玻璃面的处射向玻璃面的处,但从玻璃面的处射出时发生了折射,使光线从变成了 , 为光线延长线上一点,已知 , , 则的度数为 .
三、解答题:共8题,共78分
-
18. 在同一平面内有5条互不重合的直线,共有6个不同的交点,画出它们可能的位置关系.(画出三种不同的示意图,并指出其中互相平行的直线)19. 如图, , 点E在AC上,连接DE,请仅用无刻度直尺作图.(保留作图痕迹)
 (1)、在图1中作出一个与互补的角.(2)、在图2中,在CD的上方,作出一个与相等的角.20. 请将下列证明过程补充完整:
(1)、在图1中作出一个与互补的角.(2)、在图2中,在CD的上方,作出一个与相等的角.20. 请将下列证明过程补充完整:已知:如图,平分 , 平分 , 且 . 求证: .

证明:平分 ,
( )
平分(已知),
▲ ( ).
( ).
即 .
(已知),
▲ ( ).
▲ ( ).
21. 如图,直线AB、CD相交于点O , , 垂足为点O. (1)、 若 , 则°;(2)、若与的度数比为 , 求的度数.22. 下面是小红根据老师的要求进行的分析及解答过程,请你补全解答过程.
(1)、 若 , 则°;(2)、若与的度数比为 , 求的度数.22. 下面是小红根据老师的要求进行的分析及解答过程,请你补全解答过程.条件及问题
思路方法
解答过程
知识要素
如图,直线相交于点 ,
的角平分线,
, 求的度数.


因为 ,
所以 ,
因为 ,
所以 ,
又因为平分 ,
所以
因为 ,
所以 ,
则
垂直的定义
角平分线的定义
互为余角的定义
对顶角的性质
23. 在综合与实践课上,老师以“两条平行线 , 和一块含角的直角三角尺”为主题开展数学活动. (1)、如图①,若直角三角尺的角的顶点放在上, , 求的度数;(2)、如图②,小颖把直角三角尺的两个锐角的顶点 , 分别放在和上,请你探索与之间的数量关系并说明理由.24. 如图,AB∥CD,试探讨四个图形中∠APC与∠PAB,∠PCD的数量关系.
(1)、如图①,若直角三角尺的角的顶点放在上, , 求的度数;(2)、如图②,小颖把直角三角尺的两个锐角的顶点 , 分别放在和上,请你探索与之间的数量关系并说明理由.24. 如图,AB∥CD,试探讨四个图形中∠APC与∠PAB,∠PCD的数量关系.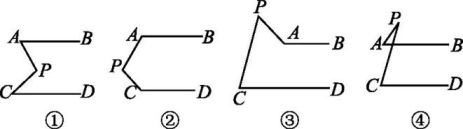 (1)、图①中∠APC与∠PAB,∠PCD的数量关系是;(2)、图②中∠APC与∠PAB,∠PCD的数量关系是;(3)、请你在图③和图④中任选一个,说出∠APC与∠PAB,∠PCD的数量关系,并说明理由.25. 如图,已知 , . 点P是射线AM上一动点(与点A不重合)、BC , BD分别平分和 , 分别交射线AM于点C , D .
(1)、图①中∠APC与∠PAB,∠PCD的数量关系是;(2)、图②中∠APC与∠PAB,∠PCD的数量关系是;(3)、请你在图③和图④中任选一个,说出∠APC与∠PAB,∠PCD的数量关系,并说明理由.25. 如图,已知 , . 点P是射线AM上一动点(与点A不重合)、BC , BD分别平分和 , 分别交射线AM于点C , D . (1)、求的度数.(2)、当点P运动到使时,的度数是多少?为什么?(3)、当点P运动时,与之间的数量关系是否随之发生变化?若不变化.请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(1)、求的度数.(2)、当点P运动到使时,的度数是多少?为什么?(3)、当点P运动时,与之间的数量关系是否随之发生变化?若不变化.请写出它们之间的关系,并说明理由;若变化,请写出变化规律.