【培优卷】4.2平行线同步练习——华师大版（2024）数学七年级上册

试卷更新日期：2024-11-17 类型：同步测试

进入出卷网下载

一、复习巩固

1. 下列说法中：①同位角相等；②在同一平面内，过一点有且只有一条直线与已知直线垂直；③过直线外一点有且只有一条直线与已知直线平行；④三条直线两两相交，总有三个交点；⑤若 $a / / b$ ，b//c，则a//c.正确的有（）

A、①②③ B、②③⑤ C、②④⑤ D、③④⑤

查看试题解析
2. 如图，下列条件中，能判定 $A D / / B C$ 的是( )

A、 $∠ C = ∠ C B E$ B、 $∠ A + ∠ A D C = 180 °$ C、 $∠ A B D = ∠ C D B$ D、 $∠ A = ∠ C B E$

查看试题解析
3. 如果两个角的两边分别平行，其中一个角是50°，则另一个角是（）

A、50° B、130° C、50°或130° D、40°

查看试题解析
4. 杆秤是中国古老的称量工具，在我国已经使用了数千年．如图，是杆秤在称物时的状态，G其中辞纽AB和拴秤砣的细线CD都是铅垂线．若 $∠ 1 = 108 °$ ，则 $∠ 2$ 的度数为（）

A、 $72 °$ B、 $108 °$ C、 $62 °$ D、 $82 °$

查看试题解析
5. 如图，光在不同介质中的传播速度不同，因此当光线从空气射向水中时，会发生折射．在空气中平行的两条入射光线，在水中的两条折射光线也是平行的，若水面和杯底互相平行，且 $∠ 1 = 122 °$ ，则 $∠ 2$ 的度数为（）

A、 $38 °$ B、 $48 °$ C、 $58 °$ D、 $68 °$

查看试题解析
6. 张老师出了一道判断题“若 $P C ∥ A B ， Q C ∥ A B$ ，则点 $P ， C ， Q$ 在一条直线上”，点点认为对．你认为点点的理由是：.

查看试题解析
7. 如图，利用三角尺和直尺可以准确地画出直线 $A B ∥ C D$ ，正确的操作顺序应该是：
①沿三角尺的边作出直线 $C D$ ；
②用直尺紧靠三角尺的另一条边；
③作直线 $A B$ ，并用三角尺的一条边贴住直线 $A B$ ；
④沿直尺下移三角尺．

查看试题解析
8. 生活中常见一种折叠拦道闸，如图1所示．若想求解某些特殊状态下的角度，需将其抽象为几何图形，如图2所示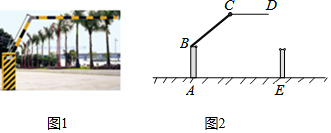， $B A$ 垂直于地面 $A E$ 于 $A$ ， $C D$ 平行于地面 $A E$ ，则 $∠ A B C + ∠ B C D =$ $° .$

查看试题解析
9. 完成下面的证明：
已知：如图，已知 $A B ∥ E F$ ， $E P ⊥ E Q$ ， $∠ 1 + ∠ A P E = 90 °$ ，
求证： $A B ∥ C D$ .
证明：∵ $A B ∥ E F$ .
∴ $∠ A P E = ∠$     ▲    （），
∵ $E P ⊥ E Q$ ， ∴ $∠ P E Q =$     ▲     ，
即 $∠ 2 + ∠ 3 = 90 °$ ， ∴ $∠ A P E + ∠ 3 = 90 °$ ，
∵ $∠ 1 + ∠ A P E = 90 °$ ， ∴ $∠ 1 = ∠$     ▲    （），
∴    ▲     $∥ C D$ （），
又∵ $A B ∥ E F$ ，
∴ $A B ∥ C D$ （）.

查看试题解析
10. 如图， $△ A B C$ 中，点 $D$ 在 $B C$ 边上.

(1)、在 $A C$ 边上求作点 $E$ ，使得 $∠ C D E = ∠ A B C$ ；（要求：尺规作图，不写作法，保留作图痕迹）

(2)、在 (1) 的条件下，若 $∠ A = 65^{\circ}$ ，求 $∠ A E D$ 的度数.

查看试题解析
11. 如图，已知∠A=∠AGE，∠D=∠DGC．

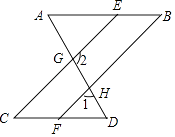(1)、求证：AB∥CD；

(2)、若∠2+∠1=180°，且∠BEC=2∠B+30°，求∠C的度数．

查看试题解析
12.

(1)、如图1，已知 $A B ∥ C D$ ， $∠ A B C = 45 °$ ，可得 $∠ B C D =$ 度；

(2)、如图2，在（1）的条件下，如果 $C M$ 平分 $∠ B C D$ ，求 $∠ E C M$ 度数；

(3)、如图3，在（1）（2）的条件下，如果 $C N ⊥ C M$ ，求 $∠ B C N$ 的度数；

(4)、尝试解决下面问题：如图4， $A B ∥ C D$ ， $∠ B C M = 20 °$ ， $C N$ 是 $∠ B C E$ 的平分线， $C N ⊥ C M$ ，求 $∠ B$ 的度数．

查看试题解析

二、能力提升

13. $l_{1}$ 、 $l_{2}$ 、 $l_{3}$ 为同一平面内的三条直线，若 $l_{1}$ 与 $l_{2}$ 不平行， $l_{2}$ 与 $l_{3}$ 不平行，那么下列判断正确的是（）

A、 $l_{1}$ 与 $l_{3}$ 一定不平行 B、 $l_{1}$ 与 $l_{3}$ 一定平行 C、 $l_{1}$ 与 $l_{3}$ 一定互相垂直 D、 $l_{1}$ 与 $l_{3}$ 可能相交或平行

查看试题解析
14. 一副三角板按如图所示叠放在一起，其中点 $B$ 、 $D$ 重合，若固定三龟板 $A O B$ ，三角板 $A C D$ 绕点 $A$ 在平面内旋转，当 $∠ B A D =$ （）时， $C D ∥ A B$ ．

A、 $90 °$ B、 $120 °$ 或 $60 °$ C、 $150 °$ 或 $30 °$ D、 $135 °$ 或 $45 °$

查看试题解析
15. 已知题目：“直线a∥b ，直线l⊥b ，垂足为A ， l交a于点B ，点C在直线b上，且在直线l的左侧．在直线a上取一点D ，连接CD ，过点D作DE⊥CD ，交直线l于点E ．若∠BDE＝30°，求∠ACD的度数．”嘉嘉画出了如图所示的图形，并求出∠ACD＝60°，而淇淇说：“嘉嘉考虑的不周全”，下列判断正确的是（）

A、淇淇说得对，且∠ACD的另一个值是120° B、淇淇说的不对，∠ACD就得60° C、嘉嘉求的结果不对，∠ACD应得50° D、两人都不对，∠ACD应有3个不同值

查看试题解析
16. 如图，已知 $A M ∥ B N$ ， $∠ A = 64 °$ ，点P是射线 $A M$ 上一动点（与点A不重合）， $B C$ 、 $B D$ 分别平分 $∠ A B P$ 和 $∠ P B N$ ，分别交射线 $A M$ 于点C、D，下列结论：① $∠ A C B = ∠ C B N$ ；② $∠ C B D = 58 °$ ；③当 $∠ A C B = ∠ A B N$ 时， $∠ A B C = 29 °$ ；④当点P运动时， $∠ A P B ： ∠ A D B = 2 ： 1$ 的数量关系不变．其中正确结论有（　　）个

A、1 B、2 C、3 D、4

查看试题解析
17. 如图，已知直线 $A B$ ， $C D$ 被直线 $E F$ 所截， $A B ∥ C D$ ，点 $P$ 是平面内位于直线 $E F$ 右侧的一个动点（点 $P$ 不在直线 $A B$ ， $C D$ 上）．设 $∠ B G P = α$ ， $∠ D H P = β$ ，在点 $P$ 的运动过程中， $∠ P$ 的度数可能是．（结果用含 $α$ ， $β$ 的式子表示）

查看试题解析
18.

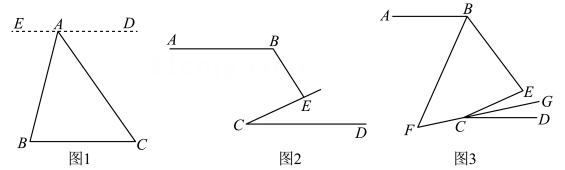(1)、阅读并补全上述推理过程.
如图1，已知点A是BC外一点，连接AB，AC.求 $∠ B A C + ∠ B + ∠ C$ 的度数.
解：过点 $A$ 作 $E D / / B C$ ，
$∴ ∠ B =______________$ ， $∴ ∠ C =______________$ ，
又 $∵ ∠ E A B + ∠ B A C + ∠ D A C = 18 0^{°}$ .
$∴ ∠ B + ∠ B A C + ∠ C =________.$
从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将 $∠ B A C, ∠ B, ∠ C$ “凑”在一起，得出角之间的关系，使问题得以解决.

(2)、如图2所示，已知 $A B / / C D, B E 、 C E$ 交于点E，∠BEC=85°，在图2的情况下求∠B-∠C的度数.

(3)、如图3，已知 $A B / / C D, B E 、 C E$ 交点E，BF、CG分别平分 $∠ A B E 、 ∠ E C D$ ，直线BF与直线CG交于点 $F$ ，若 $∠ F = 4 2^{°}$ ，则∠BEC=.

查看试题解析
19. 已知直线 $M N / / P Q$ ，点 $A$ 在直线MN上，点B、C为平面内两点， $A C ⊥ B C$ 于点 $C$ .

(1)、如图1，当点 $B$ 在直线MN上，点 $C$ 在直线MN上方时，CB交PQ于点 $D$ ，求证： $∠ C A B + ∠ C D P = 90 °$ ；

(2)、如图2，当点 $C$ 在直线MN上且在点 $A$ 左侧，点 $B$ 在直线MN与PQ之间的，过点 $B$ 作 $B D ⊥ A B$ 交直线PQ于点 $D$ ，请猜测 $∠ A B C$ 与 $∠ B D P$ 的数量关系，并说明理由；

(3)、如图3，当点 $C$ 在直线MN上，且在点 $A$ 左侧，点 $B$ 在直线PQ下方时，过点 $B$ 作 $B D ⊥ A B$ 交直线PQ于点 $D$ ，作 $∠ A B D$ 的平分线交直线MN于点 $E$ ，当 $∠ B D P = 2$ $∠ B E N$ 时，求出 $∠ A B C$ 的度数.

查看试题解析

三、拓广探索

20. 在同一平面内有 $2026$ 条直线 $a_{1}, a_{2}, . . ., a_{2026}$ ，如果 $a_{1} ∥ a_{2}, a_{2} ⊥ a_{3}, a_{3} ∥ a_{4}, a_{4} ⊥ a_{5}, . . .$ ，依此类推，那么 $a_{1}$ 与 $a_{2026}$ 的位置关系是（）

A、垂直 B、平行 C、垂直或平行 D、重合

查看试题解析
21. 课题学习：平行线的“等角转化”功能.

(1)、阅读理解：如图1，已知点A是 $B C$ 外一点，连接 $A B$ 、 $A C$ ，求 $∠ B + ∠ B A C + ∠ C$ 的度数.阅读并补充下面推理过程.
解：过点A作 $E D ∥ B C$ ，
$∴$ $∠ B =$ ▲ ， $∠ C$ ▲ ，
$∵$ $∠ E A B + ∠ B A C + ∠ D A C = 180 °$ ，
$∴$ $∠ B + ∠ B A C + ∠ C = 180 °$ .

(2)、方法运用：如图2，已知 $A B ∥ E D$ ，求 $∠ B + ∠ B C D + ∠ D$ 的度数；

(3)、深化拓展：已知 $A B ∥ C D$ ，点C在点D的右侧， $∠ A D C = 50 °$ ， $B E$ 平分 $∠ A B C$ ， $D E$ 平分 $∠ A D C$ ， $B E$ ， $D E$ 所在的直线交于点E，点E在直线 $A B$ 与 $C D$ 之间.
①如图3，点B在点A的左侧，若 $∠ A B C = 36 °$ ，求 $∠ B E D$ 的度数.
②如图4，点B在点A的右侧，且 $A B < C D$ ， $A D < B C$ .若 $∠ A B C = n °$ ，求 $∠ B E D$ 度数.（用含n的代数式表示）

查看试题解析

【培优卷】4.2平行线 同步练习——华师大版（2024）数学七年级上册

一、复习巩固

二、能力提升

三、拓广探索

【培优卷】4.2平行线同步练习——华师大版（2024）数学七年级上册