初中数学《相似》练习题
试卷更新日期:2017-12-07 类型:单元试卷
一、单选题
-
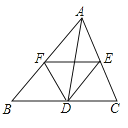
1. 如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
 A、△BDF∽△BEC B、△BFA∽△BEC C、△BAC∽△BDA D、△BDF∽△BAE2. 若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )A、增加了10% B、减少了10% C、增加了(1+10%) D、没有改变3. 矩形的两边长分别为a、b,下列数据能构成黄金矩形的是( )A、a=4,b= +2 B、a=4,b= ﹣2 C、a=2,b= +1 D、a=2,b= ﹣14. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
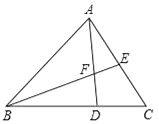
A、△BDF∽△BEC B、△BFA∽△BEC C、△BAC∽△BDA D、△BDF∽△BAE2. 若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )A、增加了10% B、减少了10% C、增加了(1+10%) D、没有改变3. 矩形的两边长分别为a、b,下列数据能构成黄金矩形的是( )A、a=4,b= +2 B、a=4,b= ﹣2 C、a=2,b= +1 D、a=2,b= ﹣14. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )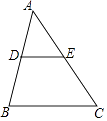 A、6 B、12 C、18 D、245. 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
A、6 B、12 C、18 D、245. 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:①AM=AD+MC;②AM=DE+BM;③DE2=AD•CM;④点N为△ABM的外心.其中正确的个数为( )
 A、1个 B、2个 C、3个 D、4个6. 如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )
A、1个 B、2个 C、3个 D、4个6. 如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )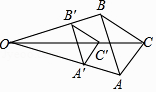 A、2:3 B、3:2 C、4:5 D、4:97. 如图,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① = ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A、2:3 B、3:2 C、4:5 D、4:97. 如图,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:① = ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )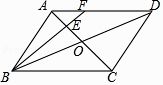 A、①②③④ B、①④ C、②③④ D、①②③8. 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
A、①②③④ B、①④ C、②③④ D、①②③8. 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ﹣2.
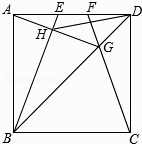 A、2 B、3 C、4 D、59. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )
A、2 B、3 C、4 D、59. 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )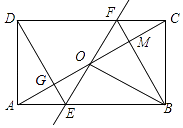 A、4个 B、3个 C、2个 D、1个10. 如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( )
A、4个 B、3个 C、2个 D、1个10. 如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( ) A、51米 B、59米 C、88米 D、174米11. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
A、51米 B、59米 C、88米 D、174米11. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )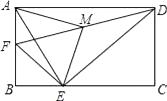 A、5 B、 C、 D、12.
A、5 B、 C、 D、12.如图,已知在 中, , , ,点 是 的重心,则点 到 所在直线的距离等于( )
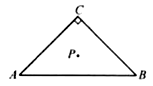 A、 B、 C、 D、13.
A、 B、 C、 D、13.如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )
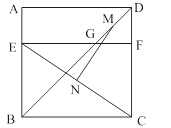 A、3 B、 C、 D、414.
A、3 B、 C、 D、414.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
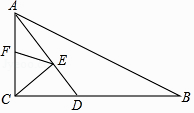 A、 B、 C、 D、615. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
A、 B、 C、 D、615. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形16.
A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形16.已知函数y= 的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
①若点M1(x1 , y1),M2(x2 , y2)在图象上,且x1<x2<0,则y1<y2;
②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;
③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;
④当点P移动到使∠AOB=90°时,点A的坐标为(2 ,﹣ ).
其中正确的结论个数为( )
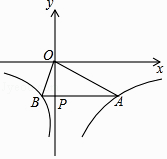 A、1 B、2 C、3 D、417. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE= ;④AF=2 ,其中正确结论的个数有( )
A、1 B、2 C、3 D、417. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE= ;④AF=2 ,其中正确结论的个数有( )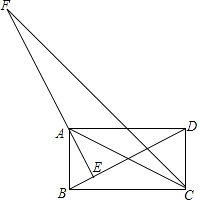 A、1个 B、2个 C、3个 D、4个18. 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )
A、1个 B、2个 C、3个 D、4个18. 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )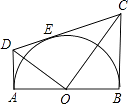 A、2个 B、3个 C、4个 D、5个19. 如图,在反比例函数y= 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 的图象上运动,若tan∠CAB=2,则k的值为( )
A、2个 B、3个 C、4个 D、5个19. 如图,在反比例函数y= 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 的图象上运动,若tan∠CAB=2,则k的值为( )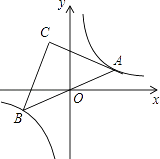 A、﹣3 B、﹣6 C、﹣9 D、﹣1220. 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG= S△FGH . 其中正确的是( )
A、﹣3 B、﹣6 C、﹣9 D、﹣1220. 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG= S△FGH . 其中正确的是( )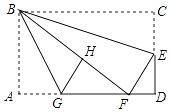 A、1个 B、2个 C、3个 D、4个21. 如果把三角形的三边按一定的比例扩大,则下列说法正确的是( )A、三角形的形状不变,三边的比变大 B、三角形的形状变,三边的比变大 C、三角形的形状变,三边的比不变 D、三角形的形状不变,三边的比不变22. 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 .其中,正确的结论是( )
A、1个 B、2个 C、3个 D、4个21. 如果把三角形的三边按一定的比例扩大,则下列说法正确的是( )A、三角形的形状不变,三边的比变大 B、三角形的形状变,三边的比变大 C、三角形的形状变,三边的比不变 D、三角形的形状不变,三边的比不变22. 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 .其中,正确的结论是( )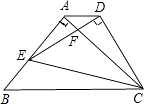 A、①②④ B、①③⑤ C、②③④ D、①④⑤23. 下列说法错误的是( )A、任意两个直角三角形一定相似 B、任意两个正方形一定相似 C、位似图形一定是相似图形 D、位似图形每一组对应点到位似中心的距离之比都等于位似比24.
A、①②④ B、①③⑤ C、②③④ D、①④⑤23. 下列说法错误的是( )A、任意两个直角三角形一定相似 B、任意两个正方形一定相似 C、位似图形一定是相似图形 D、位似图形每一组对应点到位似中心的距离之比都等于位似比24.如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )
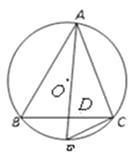 A、3个 B、2个 C、1个 D、0个25. 如图,正方形BODC的顶点C的坐标是(3,3),以原点O为位似中心,将正方形BODC缩小后得到正方形B'ODC',点C的对应点C'的坐标为(﹣1,﹣1),那么点D的对应点D'的坐标为( )
A、3个 B、2个 C、1个 D、0个25. 如图,正方形BODC的顶点C的坐标是(3,3),以原点O为位似中心,将正方形BODC缩小后得到正方形B'ODC',点C的对应点C'的坐标为(﹣1,﹣1),那么点D的对应点D'的坐标为( )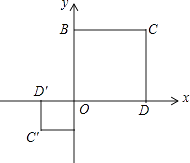 A、(﹣1,0) B、(0,﹣1) C、(1,0) D、(0,1)
A、(﹣1,0) B、(0,﹣1) C、(1,0) D、(0,1)