【培优卷】4.1相交线 同步练习——华师大版数学七年级上册
试卷更新日期:2024-11-17 类型:同步测试
一、复习巩固
-
1. 如图,∠1和∠2是对顶角的图形是( )A、
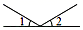 B、
B、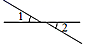 C、
C、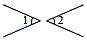 D、
D、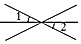 2. 如图,当剪刀口∠AOB 增大20°时,∠COD的度数( )
2. 如图,当剪刀口∠AOB 增大20°时,∠COD的度数( ) A、减小20° B、减小10° C、增大20° D、不变3.
A、减小20° B、减小10° C、增大20° D、不变3.如图,这是一条马路上的人行横道线,即斑马线的示意图,请你根据图示判断,在过马路时三条线路AC、AB、AD中最短的是( )
 A、AC B、AB C、AD D、不确定4. 如图,直线 相交于点 , 平分 , ,则 度数为( )
A、AC B、AB C、AD D、不确定4. 如图,直线 相交于点 , 平分 , ,则 度数为( ) A、125° B、130° C、135° D、145°5. 如图,与相交于点 , , 垂足为 , 若 , 则( )
A、125° B、130° C、135° D、145°5. 如图,与相交于点 , , 垂足为 , 若 , 则( ) A、44° B、46° C、134° D、136°6.
A、44° B、46° C、134° D、136°6.如图,下列说法错误的是( )
 A、∠A与∠B是同旁内角 B、∠3与∠1是同旁内角 C、∠2与∠3是内错角 D、∠1与∠2是同位角7. 如图所示的四个图形中,∠1和∠2是同位角的是( )
A、∠A与∠B是同旁内角 B、∠3与∠1是同旁内角 C、∠2与∠3是内错角 D、∠1与∠2是同位角7. 如图所示的四个图形中,∠1和∠2是同位角的是( )
 A、②③ B、①②③ C、①②④ D、①④8. 如图,直线 , 被直线所截,交点分别是点 , 点 , 则与是( )
A、②③ B、①②③ C、①②④ D、①④8. 如图,直线 , 被直线所截,交点分别是点 , 点 , 则与是( )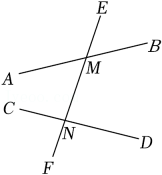 A、同位角 B、内错角 C、同旁内角 D、邻补角9. 下列说法:①如果∠1+ ∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角;②如果∠A+ ∠B=90°,那么∠A与∠B互为余角;③“对顶角相等”成立,反之“相等的角是对顶角”也成立;④两条直线被第三条直线所截,同位角相等;⑤两点之间,线段最短. 正确的个数是( )A、2个 B、3个 C、4个 D、5个10. 若∠1和∠2是对顶角,∠1=35°,则∠2的补角是 .11. 如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3等于 .
A、同位角 B、内错角 C、同旁内角 D、邻补角9. 下列说法:①如果∠1+ ∠2+∠3=180°,那么∠1,∠2,∠3三个角互为补角;②如果∠A+ ∠B=90°,那么∠A与∠B互为余角;③“对顶角相等”成立,反之“相等的角是对顶角”也成立;④两条直线被第三条直线所截,同位角相等;⑤两点之间,线段最短. 正确的个数是( )A、2个 B、3个 C、4个 D、5个10. 若∠1和∠2是对顶角,∠1=35°,则∠2的补角是 .11. 如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3等于 .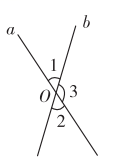 12. 为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是 .
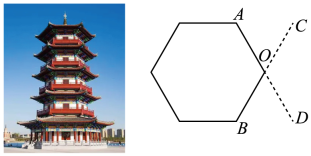
12. 为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是 .
 13. 如图,直线与相交于点B , , , 则的度数是 .
13. 如图,直线与相交于点B , , , 则的度数是 . 14. 如图,直线与相交于点O, , 若 , 则;
14. 如图,直线与相交于点O, , 若 , 则; 15.
15.如图,如果∠1=40°,∠2=100°,∠3的同旁内角等于 .
 16.
16.如图,直线 AB,CD 相交于点 O,OE 平分∠AOD,OF⊥OC,
 (1)、图中∠AOF 的余角是(把符合条件的角都填出来);(2)、如果∠AOC=160°,那么根据 , 可得∠BOD=度;(3)、如果∠1=32°,求∠2 和∠3 的度数.
(1)、图中∠AOF 的余角是(把符合条件的角都填出来);(2)、如果∠AOC=160°,那么根据 , 可得∠BOD=度;(3)、如果∠1=32°,求∠2 和∠3 的度数.
17. 两条直线被第三条直线所截,构成八个角, 即“三线入角”. (1)、两个角都在第三条直线的同旁, 并且位于两条直线的同一侧,这样的一对角叫做 , 如图中的:。(2)、两个角分别位于第三条直线的异侧, 并且都在两条直线之间, 这样的一对角叫做 , 如图中的:。(3)、两个角都在第三条直线的同旁, 并且在两条直线之间, 这样的一对角叫做, 如图中的:18. 如图所示,
(1)、两个角都在第三条直线的同旁, 并且位于两条直线的同一侧,这样的一对角叫做 , 如图中的:。(2)、两个角分别位于第三条直线的异侧, 并且都在两条直线之间, 这样的一对角叫做 , 如图中的:。(3)、两个角都在第三条直线的同旁, 并且在两条直线之间, 这样的一对角叫做, 如图中的:18. 如图所示, (1)、 和 是 , 被所截得的角;(2)、 和 是 被所截得的内错角;(3)、 和 是 被 所截而成的同旁内角;(4)、 和 是 被 所截得的内错角.
(1)、 和 是 , 被所截得的角;(2)、 和 是 被所截得的内错角;(3)、 和 是 被 所截而成的同旁内角;(4)、 和 是 被 所截得的内错角.二、能力提升
-
19. 如图,将一副三角板按不同位置摆放,其中和不一定相等的是( )A、
 B、
B、 C、
C、 D、
D、 20. 如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的个数为( )
20. 如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的个数为( )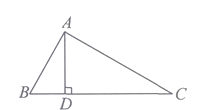
①AB⊥AC; ②AD与AC互相垂直; ③点C到AB的垂线段是线段AB;
④点A到BC的距离是线段AD的长度; ⑤线段AB的长度是点B到AC的距离;
⑥AD+BD>AB.
A、2个 B、3个 C、4个 D、5个21. 如图,点 , , , 且 , , 则与是( ) A、 B、 C、 D、22. 如图,P是直线l外一点,A , B , C三点在直线l上,且于点B , , 则下列结论中正确的是( )
A、 B、 C、 D、22. 如图,P是直线l外一点,A , B , C三点在直线l上,且于点B , , 则下列结论中正确的是( )①线段的长度是点P到直线l的距离;②线段是A点到直线的距离;③在三条线段中,最短;④线段的长度是点P到直线l的距离
 A、①②③ B、③④ C、①③ D、①②③④23. 如图,如果∠2=100°,那么∠1的同位角等于 , ∠1的内错角等于 , ∠1的同旁内角等于 .
A、①②③ B、③④ C、①③ D、①②③④23. 如图,如果∠2=100°,那么∠1的同位角等于 , ∠1的内错角等于 , ∠1的同旁内角等于 . 24. 如图,直线、相交于点O,于点O,平分.
24. 如图,直线、相交于点O,于点O,平分.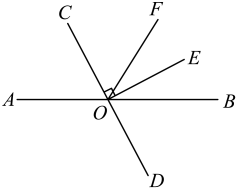 (1)、若 , 求的度数;(2)、若 , 直接写出的度数(用含的式子表示).25. 如图,汽车站、高铁站分别位于A、B两点,直线a和b分别表示公路与铁路.
(1)、若 , 求的度数;(2)、若 , 直接写出的度数(用含的式子表示).25. 如图,汽车站、高铁站分别位于A、B两点,直线a和b分别表示公路与铁路.
⑴从汽车站到高铁站怎样走最近?画出图形,理由是 ▲ .
⑵从高铁站到公路怎样走最近?画出图形,理由是 ▲ .
26. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想. (1)、如图1,直线 , 被直线 所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角.(4)、平面内n条直线两两相交,最多可以形成对同旁内角.
(1)、如图1,直线 , 被直线 所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角.(4)、平面内n条直线两两相交,最多可以形成对同旁内角.三、拓展应用
-
27. 如图,两条直线相交,有一个交点. 三条直线相交,最多有多少个交点? 四条直线呢? 你能发现什么规律?


