浙江省温州市瑞安六校联考2024-2025学年八年级上学期数学期中试卷

试卷更新日期：2024-11-15 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1. 2024年第33届奥运会在巴黎圆满落幕，下列历届奥运会会徽中属于轴对称图形的是( 　)

A、 B、 C、 D、

查看试题解析
2. 在△ABC中，∠A＝60°，∠B＝20°，则∠C的度数为( 　)

A、80° B、90° C、100° D、110°

查看试题解析
3. 四根木棒的长度分别为12cm，8cm，6cm，5cm．从中取三根，使它们首尾顺次相接组成一个三角形．则下列取法中不能组成一个三角形的是( 　)

A、12cm，8cm，6cm B、12cm，8cm，5cm C、12cm，6cm，5cm D、8cm，6cm，5cm

查看试题解析
4. 如图，△AOC与△BOD全等．已知∠A与∠B是对应角，则对其余对应边或对应角判断错误的是( 　)

A、对应边：OA与OB B、对应边：AC与BD C、对应角：∠OCA与∠ODB D、对应角：∠AED与∠BEC

查看试题解析
5. 下列命题的逆命题是假命题的是( 　)

A、等腰三角形的两个底角相等 B、内错角相等，两直线平行 C、对顶角相等 D、等边三角形的三个角都是60°

查看试题解析
6. 具备下列条件的△ABC中，不是直角三角形的是( 　)

A、三边的长度分别为1，2， $\sqrt{5}$ B、∠A ， ∠B ， ∠C的度数比为5∶12∶13 C、∠A＝∠B＋∠C D、∠B＝∠C＝45°

查看试题解析
7. 在Rt△ABC中，∠C＝90°，以A为圆心，适当长为半径画弧，交AC ， AB于D ， E两点，再分别以D ， E为圆心，大于DE的长为半径画弧，两弧交于点M ．作射线AM交BC于点F ，若BF＝5，BC＝9，则点F到AB的距离为( 　)

A、3 B、4 C、4.5 D、5

查看试题解析
8. 如图钢架中，∠A＝25°，焊上等长的钢条 $P_{1}^{} P_{2}^{}$ ， $P_{2}^{} P_{3}^{}$ …来加固钢架．若 $P_{1}^{} A = P_{1}^{} P_{2}^{}$ ，问这样的钢条至多需要的根数为( 　)

A、2根 B、3根 C、4根 D、5根

查看试题解析
9. 如图，AD是△ABC的中线，DE⊥AC ， DF⊥AB ， E ， F分别是垂足．已知AB＝2AC ， DE＝12，则DF的长度为( 　)

A、3 B、4 C、6 D、8

查看试题解析
10. 将两个等边三角形△AGF和△DEF按如图方式放置在等边三角形ABC内．若求四边形ABEF和三角形DGF的周长差，则只需知道( 　)

A、线段AD的长 B、线段EF的长 C、线段FH的长 D、线段DG的长

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分）

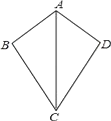
11. 命题“两直线平行，同旁内角互补”的逆命题是．

查看试题解析
12. 若△ABC≌△DEF ， A与D ， B与E分别是对应顶点，AB＝2，BC＝3，AC=4，则DF＝．

查看试题解析
13. 如图，已知AB=AD那么添加一个条件后，可判定△ABC≌△ADC．

查看试题解析
14. 将一副三角板如图摆放，则∠1＝度．

查看试题解析
15. 若等腰三角形的两边长分别是5和8，则其周长是．

查看试题解析
16. 如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙底端C的距离为0.7米．当梯子的顶端沿墙面下滑米后，梯子处于 $A_{1}^{} B_{1}^{}$ 位置，恰与原位置AB关于墙角∠ACB的角平分线所在的直线轴对称。

查看试题解析
17. 如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，分别以四边形ABCD的四条边为斜边，向外作四个等腰直角三角形，记阴影部分面积分别为 $S_{1}^{}$ ， $S_{2}^{}$ ， $S_{3}^{}$ 和 $S_{4}^{}$ ．若 $S_{1}^{} = 8$ ， $S_{2}^{} = 3$ ， $S_{3}^{} = 16$ ，则 $S_{4}^{}$ 的值是．

查看试题解析
18. 圆规是尺规作图必不可少的工具之一，图1是我们生活中常见的一种圆规样式．图2是根据圆规结构构造的特殊“圆规”图形．当“圆规”合拢时，点A和点E重合，点C落在线段AB上，AB＝10，∠BAF＝15°．当“圆规”展开一定角度，直立在纸面上时，∠BCD和∠CDF的度数固定不变，EF⊥AE（如图3），则此时以点A为圆心，AE长为半径所作圆的面积为．
（结果保留根号和 π ）

查看试题解析

三、解答题（本题有5小题，共46分，解答需写出必要的文字说明、演算步骤或证明过程）

19. 如图，在△ABC中，AB＝AC ， ∠A＝30°，BD是AC边上的高，求∠DBC的度数．

查看试题解析
20. 如图1，已知△ABC ，过点C作CD∥AB ，且CD＝BC.用尺规作△ECD≌△ABC ， E是边BC上一点.
小瑞：如图2．以点C为圆心，AB长为半径作弧，交BC于点E ，连结DE ，则△ECD≌△ABC ．
小安：以点D为圆心，AC长为半径作弧，交BC于点E ，连结DE ，则△ECD≌△ABC ．
小瑞：小安，你的作法有问题．
小安：哦…我明白了！

(1)、指出小安作法中存在的问题．

(2)、证明：△ECD≌△ABC.

查看试题解析
21. 如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点，PD⊥AB于D ， PE⊥AC于E ．

(1)、求证：BD＝CE；

(2)、若AB＝5，AC＝9，求AD的长．

查看试题解析
22. 通过对模型的研究学习，完成下列问题：

(1)、【模型呈现】如图1，在△ABC中，AD平分∠BAC ， AD⊥BC于点D ，
求证：D点为BC的中点

(2)、【模型应用】如图2，△ABC的面积为10，BE平分∠ABC ， AE⊥BE于E ，连结EC ，
则△BCE的面积为；(直接写出答案)

(3)、【拓展提高】如图3，在△ABC中，AB＝AC ， ∠BAC＝90°，点D是BC上一点（不与点B、C）重合， $∠ C D E = \frac{1}{2} ∠ B$ ， CE⊥DE ．求∠AFD的度数和 $\frac{C E}{D F}$ 的值．

查看试题解析
23. 如图，在△ABC中，AC＝3cm，BC＝4cm，∠ACB＝90°.点D从B点出发沿BA方向移动，移动速度为1cm/s，设移动时间为 t s.

(1)、当CD⊥AB时，求AD ， CD的长度.

(2)、当△ACD是以AD为腰的等腰三角形时，求t的值.

(3)、设点A关于直线CD的对称点为P.当点P落在直线BC上时，连结DP ，求△PDB的面积.

查看试题解析