人教版八年级上学期数学课时进阶测试14.2乘法公式（三阶）

试卷更新日期：2024-11-13 类型：同步测试

进入出卷网下载

一、选择题

1. 若 $a^{4} + b^{4} + a^{2} b^{2} = 5$ ， $a b = 2$ ，则 $a^{2} + b^{2}$ 的值是（）

A、－2 B、2 C、3 D、±3

查看试题解析
2. $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1)$ 的计算结果的个位数字是（）

A、8 B、6 C、2 D、0

查看试题解析
3. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{1010} + 1)$ 化简的结果为（）

A、 $2^{1010} - 1$ B、 $2^{1010} + 1$ C、 $2^{2020} - 1$ D、 $2^{2020} + 1$

查看试题解析
4. 若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为40；其中5个如图2摆放，构造出一个长方形，其中阴影部分面积为100（各个小长方形之间不重叠不留空），则每个小长方形的面积为（）

A、5 B、10 C、20 D、30

查看试题解析
5. 已知 $a = 2019 x + 2019$ ， $b = 2019 x + 2020$ ， $c = 2019 x + 2021$ ，则 $a^{2} + b^{2} + c^{2} - a b - a c - b c$ 的值为 $($ ）

A、0 B、1 C、2 D、3

查看试题解析
6. 如图使用4个全等三角形与1个小正方形镶嵌而成的正方形图案已知大正方形面积为49，小正方形面积为4，若用x、y表示直角三角形的两直角边(x>y)，下列四个说法：①x²+y²=49；②x−y=2；③2xy+4=49；④x+y=9. 其中正确的是（）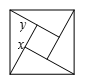

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析
7. 阅读理解：如果 $a - \frac{1}{a} = 1$ ，我们可以先将等式两边同时平方得到 ${(a - \frac{1}{a})}^{2} = 1$ ，再根据完全平方公式计算得： $a^{2} - 2 a \cdot \frac{1}{a} + \frac{1}{a^{2}} = 1$ ，即 $a^{2} - 2 + \frac{1}{a^{2}} = 1$ ，所以 $a^{2} + \frac{1}{a^{2}} = 3$ ．请运用上面的方法解决下面问题：如果 $x^{2} - 2 x - 1 = 0$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值为（）

A、8 B、6 C、4 D、2

查看试题解析

二、填空题

8. $a^{2} - 3 a + 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}}$ 的值为

查看试题解析
9. 设4x²+mx+121是一个完全平方式，则m=

查看试题解析
10. 已知 $m^{2} + n^{2} - 6 m + 10 n + 34 = 0$ ，则 $m + n$ =.

查看试题解析
11. 已知实数 $a$ 、 $b$ 满足， $| a + b - 3 | + {(a b - 2)}^{2} = 0$ ，则 $a^{2} + b^{2}$ 值为．

查看试题解析
12. 如果 $a$ ， $b$ ， $c$ 满足 $a b c \neq 0$ ， $a + b = c$ ，则 $\frac{b^{2} + c^{2} - a^{2}}{6 b c} + \frac{c^{2} + a^{2} - b^{2}}{6 a c} + \frac{a^{2} + b^{2} - c^{2}}{6 a b} =$ ．

查看试题解析

三、解答题

13. 把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积.
例如，由图①，可得等式：（a+2b）（a+b）＝a²+3ab+2b².

(1)、如图②，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来.

(2)、利用（1）中所得到的结论，解决下面的问题：
已知a+b+c＝10，a²+b²+c²＝38，求ab+bc+ac的值.

(3)、如图③，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一条直线上，连结BD和BF.若这两个正方形的边长满足a+b＝10，ab＝20，请求出阴影部分的面积.

查看试题解析