人教版九年级上学期数学课时进阶测试25.3用频率估计概率（三阶）

试卷更新日期：2024-11-11 类型：同步测试

进入出卷网下载

一、选择题（每题3分）

1. 下列说法正确的是（）

A、掷一枚质地均匀的骰子，掷得的点数为3的概率是 $\frac{1}{3}$ B、某种彩票中奖的概率是 $\frac{1}{10000}$ ，那么买10000张这种彩票一定会中奖 C、掷两枚质地均匀的硬币，“两枚硬币都是正面朝上”的概率与“一枚硬币正面朝上，一枚硬币反面朝上”的概率相同 D、通过大量重复试验，可以用频率估计概率

查看试题解析
2. 下列说法正确的个数是（）
①关于x的方程 $(a - 1) x^{a^{2} + 1} + 5 x - 2 = 0$ 是一元二次方程，则a=+1；

②二次函数y=x²-2x+1的图象与x轴只有一个公共点；

③“随时打开电视机，正在播放《感动中国》”是随机事件；

④掷一枚图钉，做大量重复试验，发现“针尖朝下”的频率稳定于0.3，则掷一次该图钉，估计“针尖朝下”的概率为0.3.

A、1 B、2 C、3 D、4

查看试题解析
3. 下列四种说法：
①如果一个角的两边与另一个角的两边分别平行，那么这两个角相等；②将2020减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，再减去余下的 $\frac{1}{5}$ ，……，依此类推，直到最后减去余下的 $\frac{1}{2020}$ ，最后的结果是1；③实验的次数越多，频率越靠近理论概率；④对于任何实数x、y ，多项式 $x^{2} + y^{2} - 4 x - 2 y + 7$ 的值不小于2．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 投掷硬币m次，正面向上n次，其频率p= $\frac{n}{m}$ ，则下列说法正确的是（）

A、p一定等于 $\frac{1}{2}$ B、p一定不等于 $\frac{1}{2}$ C、多投一次，p更接近 $\frac{1}{2}$ D、投掷次数逐步增加，p稳定在 $\frac{1}{2}$ 附近

查看试题解析
5. 某商店进行“迎五一，大促销”摸奖活动，凡是有购物小票的顾客均可摸球一次，摸到的是白球即可获奖．规则如下：一个不透明的袋子中装有10个黑球和若干白球，它们除颜色不同外，其余均相同，从袋子中随机摸出一个球，记下颜色，再把它放回袋子中摇匀，重复此过程．共有300人摸球，其中获奖的共有180人，由此估计袋子中白球个数大约为（）

A、10 B、12 C、15 D、16

查看试题解析
6. 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．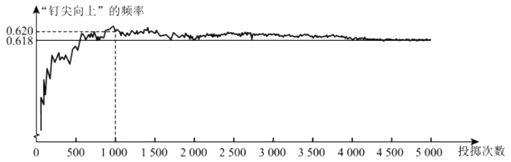
下面有三个推断：
①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；
②随着试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
③若再次用计算机模拟此实验，则当投掷次数为1000时，“钉尖向上”的频率一定是0.620．
其中合理的是（）

A、① B、② C、①② D、①③

查看试题解析

7. 小张承包了一片荒山，他想把这片荒山改造成一个橡胶园，现在有一种橡胶树树苗，它的成活率如下表所示，则下面推断中，其中合理的是（）．

移植棵数 $(n)$	成活数 $(m)$	成活率 $(m / n)$	移植棵数 $(n)$	成活数 $(m)$	成活率 $(m / n)$
50	47	$0.940$	1500	1335	$0.890$
270	235	$0.870$	3500	3203	$0.915$
400	369	0.923	7000	6335	$0.905$
750	662	$0.883$	14000	12628	$0.902$

下面有四个推断：

①小张移植3500棵这种树苗，成活率肯定高于 $0.890$ ；②随着移植棵数的增加，树苗成活的频率总在 $0.900$ 附近摆动，显示出一定的稳定性，可以估计树苗成活的概率是 $0.900$ ；③若小张移植10000棵这种树苗，则可能成活9000棵；④若小张移植20000棵这种树苗，则一定成活率18000棵．

A、①② B、①④ C、②③ D、②④

查看试题解析

二、填空题（每题3分）

8. 一个不透明的布袋中，装有红、黄、白三种只有颜色不同的小球，其中红色小球有8个，黄、白色小球的数目相等，为估计袋中黄色小球的数目，每次将袋中小球搅匀后摸出一个小球记下颜色，再次搅匀 $\dots \dots$ 多次试验发现摸到红球的频率是 $\frac{1}{6}$ ，则估计黄色小球的数目是个。

查看试题解析
9. 在创建全国文明城市活动中，衢州市园林部门为了扩大市区的绿化面积，进行了大量的树木移栽.如表记录的是在相同条件下移栽某种幼树的棵数和成活棵数：

移栽棵树

100

500

1000

5000

10000

成活棵树

89

458

910

4498

9000

请根据表中数据估计，现园林部门移栽50000棵这种幼树，大约能成活棵.

查看试题解析
10. 黑色不透明口袋里装有红色、白色球共10个，它们除颜色外都相同．从口袋中随机摸出一个球，记下颜色后放回，并摇匀，不断重复上述实验1000次，其中200次摸到红球，则可估计口袋中红色球的个数是．

查看试题解析

11. 同学们设计了一个用计算机模拟随机重复抛掷瓶盖的实验，记录盖面朝上的次数，并计算盖面朝上的频率，下表是依次累计的实验结果．

抛掷次数	500	1000	1500	2000	3000	4000	5000
盖面朝上次数	275	558	807	1054	1587	2124	2650
盖面朝上频率	0.550	0.558	0.538	0.527	0.529	0.531	0.530

下面有两个推断：

①随着实验次数的增加，“盖面朝上”的频率总在0.530附近，显示出一定的稳定性，可以估计“盖面朝上”的概率是0.530；

②若再次用计算机模拟此实验，则当投掷次数为1000时，“盖面朝上”的频率不一定是0.558；

其中合理的推断的序号是：．

查看试题解析

12. 在一个不透明的箱子里装有红色、蓝色、黄色的球共20个，除颜色外，形状、大小、质地等完全相同，小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在10%和15%，则箱子里蓝色球的个数很可能是个．

查看试题解析

三、综合题

13. 如图所示为某商场的一个可以自由转动的转盘，商场规定顾客购物满100元即可获得一次转动转盘的机会，当转盘停止时，指针落在哪一个区域就获得相应的奖品，如表是活动进行中的统计数据：
转动转盘的次数
50
100
200
500
800
1000
2000
5000
落在“纸巾”区的次数
22
71
109
312
473
612
1193
3004
根据以上信息，解析下列问题：

(1)、请估计转动该转盘一次，获得纸巾的概率是；（精确到0.1）

(2)、现有若干个除颜色外都相同的白球和黑球，根据（1）的结论，在保证获得纸巾和免洗洗手液概率不变的情况下，请你设计一个可行的摸球抽奖规则，详细说明步骤；

(3)、小明和小亮都购买了超过100元的商品，均获得一次转动转盘的机会，根据（2）中设计的规则，利用画树状图或列表的方法求两人都获得纸巾的概率．

查看试题解析

14. 在同样的条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表.

实验种子数（粒）	1	5	50	100	200	500	1000	2000	3000
发芽频数	0	4	45	92	188	476	951	1900	2850

(1)、估计该麦种的发芽概率.

(2)、如果播种该种小麦每公顷所需麦苗数为4000000棵，种子发芽后的成秧率为80%，该麦种的千粒质量为50g.那么播种3公顷该种小麦，估计约需麦种多少千克（精确到1kg）？

查看试题解析

转动转盘的次数	50	100	200	500	800	1000	2000	5000
落在“纸巾”区的次数	22	71	109	312	473	612	1193	3004

移栽棵树	100	500	1000	5000	10000
成活棵树	89	458	910	4498	9000