人教版九年级上学期数学课时进阶测试25.2用列举法求概率（三阶）

试卷更新日期：2024-11-11 类型：同步测试

进入出卷网下载

一、选择题

1. 以下说法合理的是（）

A、小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是 $\frac{2}{3}$ B、某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖 C、小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的概率还是 $\frac{1}{2}$ D、某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是 $\frac{1}{2}$

查看试题解析
2. 一个不透明的口袋中有四个完全相同的小球，把它们分别标号为2，3，4，5，若随机摸出一个小球后不放回，再随机摸出一个小球，则两次取出小球标号的积是6的倍数的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{12}$

查看试题解析
3. 一项“过关游戏”规定：在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6个点)抛掷n次，若n次抛掷所出现的向上一面的点数之和大于 $\frac{5}{4}$ n² ，则算过关；否则，不算过关．能过第二关的概率是（）．

A、 $\frac{13}{18}$ B、 $\frac{5}{18}$ C、 $\frac{1}{4}$ D、 $\frac{1}{9}$

查看试题解析
4. 甲乙两人轮流在黑板上写下不超过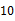的正整数（每次只能写一个数），规定禁止在黑板上写已经写过的数的约数，最后不能写的为失败者，如果甲写第一个，那么，甲写数字（）时有必胜的策略．

A、10 B、9 C、8 D、6

查看试题解析
5. 如图，甲、乙、丙三名同学比赛定点射门，PQ是球门，且甲、乙、丙三名同学位于以点O 为圆心的同一圆弧上，仅从射门角度考虑的话，进球概率最大的是（）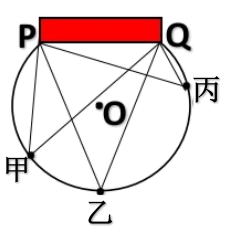

A、甲 B、乙 C、丙 D、三名同学一样大

查看试题解析
6. 我国魏晋时期的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理，如图，若 $a = 2$ ， $b = 3$ ，现随机向该图形内掷一枚小针，则针尖落在阴影区域内的概率（）．

A、 $\frac{2}{5}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析

二、填空题

7. 一个不透明的箱子里装有 $m$ 个球，其中红球4个，这些球除颜色不同其余都相同，每次搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验发现，摸到红球的频率稳定在0.25附近，则可以估算出 $m$ 的值为．

查看试题解析
8. 已知a、b、c、满足 $\frac{b}{a + c} = \frac{a}{c + b} = \frac{c}{a + b} = k$ ，从下列四点：① $(1 ， \frac{1}{2})$ ；②(2，1)；③ $(1 ， - \frac{1}{2})$ ；④(1，﹣1)，中任意取一点恰好在正比例函数y＝kx图象上的概率是.

查看试题解析
9. 在平面直角坐标系中，作△OAB，其中三个顶点分别是O(0，0)，B(1，1)，A(x，y)(－2≤x≤2，－2≤y≤2，x，y均为整数)，则所作△OAB为直角三角形的概率是．

查看试题解析

三、解答题

10. 生物学上通常用“标记重捕法”来估算特定区域内某种群的数量．如在固定区域内用捕虫网捕捉了40只田鼠，将它们标记后放回直到充分混合后，用同一个捕虫网捕捉了80只田鼠，其中有16只是被标记的，于是估算该区域田鼠的数量为：
$N = 40 \div \frac{16}{80} = 200$ （只）．
某研究小组考察了一湖泊中的某鱼种群的年龄组成，结果如下表，请回答问题：
年龄
A
B
C
D
……
个体数量
92
187
x
y
……
注：表中“ $A$ ”表示鱼的年龄 $0 - 1$ 年， $B$ 表示年龄 $2 - 3$ 年， $C$ 表示年龄 $4 - 5$ 年， $D$ 表示年龄为 $6 - 7$ 年．

(1)、年龄为 $A$ ， $B$ ， $C$ 的个体数量的平均数为125，年龄在 $A$ ， $B$ ， $C$ ， $D$ 的个体数量的中位数是95，则 $x =$ ， $y =$ （其中 $92 < y < 96$ ）．

(2)、若将年龄为 $D$ 的鱼全部标记后并放回湖泊，充分混合后，捕捉120条鱼，其中被标记鱼有12条，那么该湖泊里一共约有多少条鱼？

(3)、现捕获A，B，C，D年龄段的鱼各一条，从中任抓两条，请用列表或画树状图求抓到的是 $A$ 和 $C$ 年龄的鱼的概率．

查看试题解析
11. 已知甲同学手中藏有三张分别标有数字 $\frac{1}{2}$ ， $\frac{1}{4}$ ， 1的卡片，乙同学手中藏有三张分别标有数字1，3，2的卡片，卡片外形相同.现从甲、乙两人手中各任取一张卡片，并将它们的数字分别记为 $a ， b$ .

(1)、请你用画树状图或列表的方法列出所有可能的结果.

(2)、现制订这样一个游戏规则：若所选出的 $a ， b$ 能使得 $a x^{2} + b x + 1 = 0$ 有两个不相等的实数根，则称甲获胜；否则称乙获胜.请问：这样的游戏规则公平吗?请你用概率的知识解释.

查看试题解析

年龄	A	B	C	D	……
个体数量	92	187	x	y	……