人教版九年级上学期数学课时进阶测试25.1随机事件与概率(三阶)
试卷更新日期:2024-11-11 类型:同步测试
一、选择题
-
1. 下列事件中,属于必然事件的是( )A、在一个只装有白球和黑球的袋中摸出红球 B、一个三角形三个内角的和小于180° C、若是实数,则 D、在一张纸上任意画两条线段,这两条线段相交2. “对于二次函数 , 当时,y随x的增大而增大”,这一事件为( )A、必然事件 B、随机事件 C、不确定事件 D、不可能事件3. 中国象棋文化历史久远.在图中所示的部分棋盘中,“馬”的位置在“
 ”(图中虚线)的下方,“馬”移动一次能够到达的所有位置已用“●”标记,则“馬”随机移动一次,到达的位置在“
”(图中虚线)的下方,“馬”移动一次能够到达的所有位置已用“●”标记,则“馬”随机移动一次,到达的位置在“ ”上方的概率是( )
”上方的概率是( ) A、 B、 C、 D、4. 已知一次函数 , 从2,-3中随机取一个值,从1,-1,-2中随机取一个值,则该一次函数的图象经过第二、三、四象限的概率为( )A、 B、 C、 D、5. 下列说法中错误的是( )A、篮球队员在罚球线上投篮一次,未投中是随机事件 B、“任意画出一个平行四边形,它是中心对称图形”是必然事件 C、“抛一枚硬币,正面向上的概率为 ”表示每抛两次就有一次正面朝上 D、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近6. 如图所示,在平面直角坐标系中,点在轴上,点在轴上,坐标分别为 , 分别以四点中的任意两点与点为顶点作三角形.则所作的三角形为等腰三角形的概率是( ).
A、 B、 C、 D、4. 已知一次函数 , 从2,-3中随机取一个值,从1,-1,-2中随机取一个值,则该一次函数的图象经过第二、三、四象限的概率为( )A、 B、 C、 D、5. 下列说法中错误的是( )A、篮球队员在罚球线上投篮一次,未投中是随机事件 B、“任意画出一个平行四边形,它是中心对称图形”是必然事件 C、“抛一枚硬币,正面向上的概率为 ”表示每抛两次就有一次正面朝上 D、“抛一枚均匀的正方体骰子,朝上的点数是6的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在 附近6. 如图所示,在平面直角坐标系中,点在轴上,点在轴上,坐标分别为 , 分别以四点中的任意两点与点为顶点作三角形.则所作的三角形为等腰三角形的概率是( ).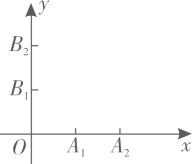 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 有四张正面分别标有数字﹣4,﹣3,﹣2,1,的不透明卡片,它们除数字不同外其他全部相同,现将它们背面朝上,洗匀后从中抽取一张,将该卡片上的数字记为a,放回后洗匀,再从中抽取一张,将该卡片上的数字记为b,则a,b使得二次函数y=x2﹣(a+5)x+3当x≤1时y随x的增大而减小,且一元二次方程(a+2)x2+bx+1=0有解的概率为 .8. 在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是.
9. 一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数5的概率是.
10. 从1,2,3,4中任取3个数,作为一个一元二次方程的系数,则构作的一元二次方程有实根的概率是。
11. 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为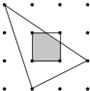
三、解答题
-
12. 某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定选n名女生.(1)、当n为何值时,男生小强参加是确定事件?(2)、当n为何值时,男生小强参加是随机事件?
四、综合题
-
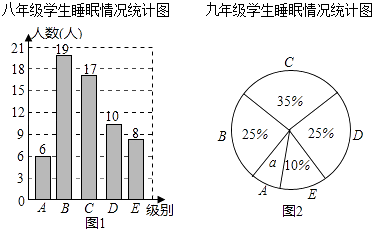
13. 为了解某校八、九年级学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如下统计图和统计表.
睡眠情况分组表(单位:时)
组别
睡眠时间x
A
4.5≤x<5.5
B
5.5≤x<6.5
C
6.5≤x<7.5
D
7.5≤x<8.5
E
8.5≤x<9.5
根据图表提供的信息,回答下列问题:
(1)、求统计图中的a;
(2)、抽取的样本中,九年级学生睡眠时间在C组的有多少人?
(3)、睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
14. 根据数学知识,完成下列问题.(1)、把长为的线段任意分成3条线段,求这3条线段能够构成一个三角形的3条边的概率.(2)、据统计,2008年底该市汽车拥有量为75万辆,而截止到2010年底,该市的汽车拥有量已达108万辆.为了保护环境,缓解汽车拥堵,该市拟控制汽车总量,要求到2012年底全市汽车拥有量不超过125.48万辆;且从2011年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的 . 假设每年新增汽车数量相同,请估算出该市从2011年初起每年新增汽车数量最多不超过多少万辆,并求出求2008年底至2010年底该市汽车拥有量的年平均增长率.
-