人教版九年级上学期数学课时进阶测试25.1随机事件与概率（二阶）

试卷更新日期：2024-11-11 类型：同步测试

进入出卷网下载

一、选择题

1. 从下列标志图中任选一张，选中既是轴对称图形又是中心对称图形的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
2. 下列说法错误的是（）.

A、在“双减”政策下，南昌外国语学校为了解九年级学生的睡眠时间，随机选择了该年级100名学生进行调查，则样本容量是100. B、“画一个正六边形，它的外角和是360°”属于必然事件. C、调查江西卫视大型综艺节目《金牌调解》节目的收视率，应采用全面调查. D、在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数可能是5个.

查看试题解析
3. 如图，我国古代数学家赵爽使用的弦图是由四个全等的直角三角形构成的正方形 $A B C D$ ，若 $A F = 4$ ， $B F = 3$ ，在弦图区域内随机取点，则该点落在正方形 $E F G H$ 区域内的概率为（）

A、 $\frac{1}{15}$ B、 $\frac{1}{20}$ C、 $\frac{1}{24}$ D、 $\frac{1}{25}$

查看试题解析
4. 在不透明的袋子里装有2个红球、3个白球、2个黑球，它们除颜色外都相同，从袋子中任意摸出1个球.下列判断正确的是（）
甲：摸到红球比摸到白球的可能性小；乙：摸到红球和摸到黑球的可能性相同

A、只有甲对 B、只有乙对 C、甲、乙都对 D、甲、乙都不对

查看试题解析
5. 从一个不透明的口袋中随机摸出一球，再放回袋中，不断重复上述过程，一共摸了150次，其中有50次摸到黑球，已知口袋中仅有黑球10个和白球若干个，这些球除颜色外，其他都一样，由此估计口袋中白球的个数约为（）

A、10 B、15 C、20 D、30

查看试题解析
6. 以下说法合理的是（）

A、小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是 $\frac{2}{3}$ B、某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖 C、某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是 $\frac{1}{2}$ D、小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的概率还是 $\frac{1}{2}$

查看试题解析
7. 在一个不透明的盒子中，装有除颜色外完全相同的乒乓球共16个，从中随机摸出一个乒乓球，若摸到黄色乒乓球的概率为 $\frac{3}{8}$ ，则该盒子中装有黄色乒乓球（）

A、5个 B、6个 C、7个 D、8个

查看试题解析

二、填空题

8. 从一个不透明的口袋中随机摸出一球，再放回袋中，不断重复上述过程，一共摸了150 次，其中有50次摸到黑球．已知口袋中仅有黑球10个和白球若干个，这些球除颜色外其他都一样，由此估计口袋中有个白球．

查看试题解析
9. 已知函数 $y = (3 k + 1) x + 5$ （ $k$ 为常数），若从 $- 3 ⩽ k ⩽ 3$ 中任取 $k$ 值，则得到的函数是具有性质“ $y$ 随 $x$ 增加而减小”的一次函数的概率为.

查看试题解析
10. 在－1，0，1这三个数中任取两个数 $m$ ， $n$ ，则二次函数 $y = {(x - m)}^{2} + n$ 图象的顶点在坐标轴上的概率为.

查看试题解析

三、解答题

11. 一个不透明的袋中装有2个白球，3个黑球，5个红球，每个球除颜色外都相同．

(1)、从中任意摸出一个球，摸到红球是事件；摸到黄球是事件；（填“不可能”或“必然”或“随机”）

(2)、从中任意摸出一个球，摸到黑球的概率；

(3)、现在再将若干个同样的黑球放入袋中、与原来10个球均匀混合在一起，使从袋中任意摸出一个球为黑球的概率为 $\frac{3}{4}$ ，请求出后来放入袋中的黑球个数．

查看试题解析
12. 综合与实践

(1)、【问题再现】
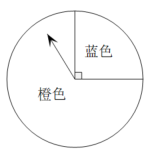
课本中有这样一道概率题：如图1，这是一个可以自由转动的转盘，转动转盘，当转盘停止时，指针落在蓝色区域和橙色区域的概率分别是多少？请你解答．

(2)、【类比设计】
在元旦晚会上班长想设计一个摇奖转盘．请你在图2中设计一个转盘，自由转动这个转盘，当它停止转动时，三等奖：指针落在红色区域的概率为 $\frac{1}{2}$ ，二等奖：指针落在白色区域的概率为 $\frac{1}{3}$ ，一等奖：指针落在黄色区域的概率为 $\frac{1}{6}$ ．

(3)、【拓展运用】
在一次促销活动中，某商场为了吸引顾客，设立转盘，转盘被平均分为10份，顾客每消费200元转动1次，对准红1份，黄2份、绿3份区域，分别得奖金100元、50元、30元购物券，求转动1次所获购物券的平均数．

查看试题解析