含参一元一次方程—人教版数学七（上）知识点训练

试卷更新日期：2024-11-10 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 方程3x－a＝8的解是x＝2，则a等于（）

A、－14 B、－2 C、2 D、14

查看试题解析
2. 若 $x = 1$ 是关于 $x$ 的方程 $3 x - 2 m = 1$ 的解，则 $m$ 的值是 $($ 　　 $)$

A、 $- 1$ B、1 C、 $- 2$ D、3

查看试题解析
3. 若方程 $2 x + 1 = - 3$ 的解是关于 $x$ 的方程 $3 x - 2 a = 6 x + 2$ 的解，则 $a$ 的值为（）

A、2 B、－2 C、－4 D、4

查看试题解析
4. 若关于 $y$ 的一元一次方程 $\frac{a + 4 y}{6} = \frac{a - 2 y}{2} + 1$ 的解是 $y = - 4$ ，则 $a$ 的值是（）

A、23 B、 $- 23$ C、 $20.5$ D、 $- 20.5$

查看试题解析
5. 小明在解关于x的一元一次方程 $\frac{x}{3} - m = \frac{1}{4}$ 时，由于粗心大意在去分母时出现漏乘错误，把原方程化为 $4 x - m = 3$ ，并解得为 $x = 1$ ，请根据以上已知条件求出原方程正确的解为（）

A、 $x = 2$ B、 $x = 1$ C、 $x = \frac{1}{12}$ D、 $x = \frac{15}{4}$

查看试题解析
6. 已知关于 $x$ 的方程 $3 x - a = 0$ 的解与关于 $x$ 的方程 $- 5 x + a + 2 = 0$ 的解互为相反数，则 $a =$ ．

查看试题解析
7. 已知x=3 是方程 $3 [(\frac{x}{3} + 1) + \frac{m (x - 1)}{4}] = 2$ 的解，求m的值.

查看试题解析
8. 已知关于x的方程 $\frac{x + a}{3} = x - \frac{a}{2}$ 与方程 $3 x + 5 = 11$ 的解互为相反数，求a的值.

查看试题解析
9. 已知 $A = 2 a^{2} - 2 a b + b^{2}$ ， $B = 3 a^{2} - 6 a b + b^{2}$ .

(1)、求 $2 A - B$ ；

(2)、若关于 $a$ 的方程 $\frac{5}{12} a - \frac{a}{4} = \frac{1}{3}$ ， $b = 3$ ，求方程 $\frac{5}{12} a - \frac{a}{4} = \frac{1}{3}$ 的解，并计算 $2 A - B$ 的值.

查看试题解析
10. 已知关于x的一元一次方程 $\frac{7 x - 1}{2} + m = 5$ ，其中m是正整数．

(1)、当 $m = 3$ 时，解这个方程；

(2)、若该方程有正整数解，求m的值

查看试题解析

二、能力提升

11. 已知x的方程2x+k=5的解为正整数，则k所能取的正整数值为（）

A、1 B、1或3 C、3 D、2或3

查看试题解析
12. 如图，数轴上A、B、C三点所表示的数分别是a，6，c，已知 $A B = 8 ， a + c$ $= 0$ ，且 $c$ 是关于 $x$ 的方程 $(m - 4) x + 16 = 0$ 的一个解，则 $m$ 的值为 $()$

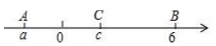A、－4 B、2 C、4 D、6

查看试题解析
13. 关于x的方程 $m x + \frac{7}{3} = x + \frac{4}{3}$ 有正整数解，则符合条件的整数m的值是．

查看试题解析
14. 若关于x的方程 $\frac{3 x}{2} + \frac{a x + 2}{3} = b$ 有无数解，则 $2 a + 3 b$ 的值为．

查看试题解析
15. 如果两个方程的解相差1，则称解较大的方程为另一个方程的“后移方程”．例如：方程 $x - 2 = 0$ 是方程 $x - 1 = 0$ 的后移方程．

(1)、判断方程 $2 x + 1 = 0$ 是否为方程 $2 x + 3 = 0$ 的后移方程（填“是”或“否”）；

(2)、若关于x的方程 $3 x + m + n = 0$ 是关于x的方程 $3 x + m = 0$ 的后移方程，求n的值．

(3)、当 $a \neq 0$ 时，如果方程 $a x + b = 0$ 是方程 $a x + c = 0$ 的后移方程，用等式表达a，b，c满足的数量关系．

查看试题解析

三、拓展创新

16. 现定义运算“*”，对于任意有理数a，b满足a*b＝ ${\begin{array}{l} 2 a - b ， a \geq b \\ a - 2 b ， a < b \end{array}$ .如5*3＝2×5﹣3＝7， $\frac{1}{2}$ *1＝ $\frac{1}{2}$ ﹣2×1＝﹣ $\frac{3}{2}$ ，若x*3＝5，则有理数x的值为（）

A、4 B、11 C、4或11 D、1或11

查看试题解析
17. 对于两个不相等的有理数 $a ， b$ ，我们规定符号 $m i n {a ， b}$ 表示 $a ， b$ 两数中较小的数，例如 $m i n {2 ， - 3} = - 3$ ．按照这个规定，方程 $m i n {x ， - x} = - 3 x - 12$ 的解为．

查看试题解析
18. 对于数 $x$ 、 $y$ ，我们定义一种新运算 $G (x, y) = \frac{1}{2} x + b y$ ，由这种运算得到的数，我们称之为“吉祥数”，记为 $G (x, y)$ ，这时 $x$ ， $y$ 叫做吉祥数对，如 $G (1,2) = \frac{1}{2} \times 1 + b \times 2 = \frac{1}{2} + 2 b$ ．

(1)、若 $G (x, y) = \frac{1}{2} x + \frac{1}{3} y$ ，则 $G (2,1) + G (\frac{3}{2}, \frac{1}{2})$ 等于多少？

(2)、已知 $G (x, y) = \frac{1}{2} x + b y$ ， $G (\frac{1}{3}, \frac{1}{2}) = 2$ ，求 $b$ 的值．

查看试题解析
19. 定义：若 $A - B = m$ ，则称 $A$ 与 $B$ 是关于 $m$ 的关联数．例如：若 $A - B = 2$ ，则称 $A$ 与 $B$ 是关于2的关联数．

(1)、若4与 $a$ 是关于7的关联数，求 $a$ 的值；

(2)、若 $2 x - 1$ 与 $3 x - 5$ 是关于6的关联数，求 $x$ 的值；

(3)、若 $M$ 与 $N$ 是关于 $m$ 的关联数， $M = 3 m n + n + 3$ ， $N$ 的值与 $m$ 无关，求 $N$ 的值．

查看试题解析
20. 定义：如果两个一元一次方程的解之和为 $1$ ，我们就称这两个方程互为“阳光方程” $.$ 例如： $2 x = 2$ 的解为 $x = 1$ ， $x + 1 = 1$ 的解为 $x = 0$ ，所以这两个方程互为“阳光方程”．

(1)、若关于 $x$ 的一元一次方程 $x + 2 m = 0$ 与 $3 x - 2 = - x$ 是“阳光方程”，则 $m =$ ．

(2)、已知两个一元一次方程互为“阳光方程”，且这两个“阳光方程”的解的差为 $5 .$ 若其中一个方程的解为 $x = k$ ，求 $k$ 的值．

(3)、 $①$ 已知关于 $x$ 的一元一次方程 $\frac{x}{2023} + a = 2023 x$ 的解是 $x = 2024$ ，请写出解是 $y = 2023$ 的关于 $y$ 的一元一次方程： $\frac{()}{2023} + 2023 ()$ $= - a . ($ 只需要补充含有 $y$ 的代数式 $)$ ．
$②$ 若关于 $x$ 的一元一次方程 $\frac{1}{2023} x - 1 = 0$ 和 $\frac{1}{2023} x - 5 = 2 x + a$ 互为“阳光方程”，则关于 $y$ 的一元一次方程 $\frac{y}{2023} - 9 - a = 2 y - \frac{2}{2023}$ 的解为．

查看试题解析