整式的加减运算—人教版数学七（上）知识点训练

试卷更新日期：2024-11-10 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 下列运算正确的是（）

A、 $(2 x - 3 y) + (5 x + 4 y) = 7 x + 7 y$ B、 $(8 a - 7 b) - (4 a - 5 b) = 4 a - 12 b$ C、 $- 5 a + (3 a - 2) - (3 a - 7) = - 5 a - 9$ D、 $\frac{1}{3} (9 y - 3) + 2 (y + 1) = 5 y + 1$

查看试题解析
2. 如果 $x_{}^{2} - 3 x = 4$ ，那么 $3 x_{}^{2} - 9 x + 8$ 的值是（）

A、-4 B、4 C、16 D、20

查看试题解析
3. 要使多项式 $2 x^{2} - 2 (7 + 3 x - 2 x^{2}) + m x^{2}$ 化简后不含 $x$ 的二次项，则 $m$ 的值是（）

A、2 B、0 C、-2 D、-6

查看试题解析
4. 计算：

(1)、 $5 a + 3 a - (2 a - a)$ ．

(2)、 $(3 x^{2} - x y - 1) - 2 (x^{2} + x y + 2)$ ．

查看试题解析
5. 设 $M = - a + 3 b$ ， $N = 3 a + b$ ，化简下列各式：

(1)、 $M + N$

(2)、 $2 M - N$

查看试题解析
6. 老师写出一个整式： $2 (a x^{2} - b x - 1) - 3 （ 2 x^{2}$ -x）-1，其中a，b为常数，且表示为系数，然后让同学们给 a，b赋予不同的数值进行计算.

(1)、甲同学给出了一组数据，然后计算的结果为 $2 x^{2} - x - 3,$ 则甲同学给出a，b的值分别是a= ， b=.

(2)、乙同学给出了a=5，b=-1，请按照乙同学给出的数值化简整式.

(3)、丙同学给出一组数，计算的最后结果与x的取值无关，请直接写出丙同学的计算结果.

查看试题解析

二、能力提升

7. 把四张形状、大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形的盒子底部，按图甲和图乙两种方式摆放，若长方体盒子底部的长与宽的差为2，则图甲和图乙中阴影部分周长之差为（）

A、4 B、3 C、2 D、1

查看试题解析
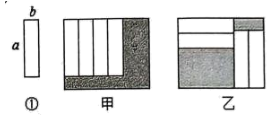8. 已知： $M = 2 a b - 3 a + 1$ ， $N = a + 3 a b - 5$ ，若 $2 M - N$ 的值与 $a$ 的取值无关，则 $b$ 的值为．

查看试题解析
9. 加查县8路公交上原有乘客 $(4 a - 2 b)$ 人，中途有一半人下车，又上车若干人，这时车上共有乘客 $(8 a - 5 b)$ 人．则中途上车的乘客有人．（用含 $a$ ， $b$ 的式子表示）

查看试题解析
10. 小马虎做一道数学题，“已知两个多项式 $A = □ x^{2} - 4 x$ ， $B = 2 x^{2} + 3 x - 4$ ，试求 $A + 2 B$ .”其中多项式 $A$ 的二次项系数印刷不清楚.

(1)、小马虎看答案以后知道 $A + 2 B = x^{2} + 2 x - 8$ ，请你替小马虎求出系数“ $□$ ”；

(2)、在（1）的基础上，小马虎已经将多项式 $A$ 正确求出，老师又给出了一个多项式 $C$ ，要求小马虎求出 $A - C$ 的结果.小马虎在求解时，误把“ $A - C$ ”看成“ $A + C$ ”，结果求出的答案为 $x^{2} - 6 x - 2$ .请你替小马虎求出“ $A - C$ ”的正确答案.

查看试题解析

三、拓展创新

11. 【阅读材料】我们知道，“整体思想”是中学数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．如 $4 a - 2 a + a = (4 - 2 + 1) a = 3 a$ ，类似地，我们把 $(x + y)$ 看成一个整体，则 $4 (x + y) - 2 (x + y) + (x + y) = (4 - 2 + 1) (x + y) = 3 (x + y)$ ．
请仿照上面的解题方法，完成下列问题：

(1)、【尝试应用】
把 ${(x - y)}^{2}$ 看成一个整体，合并 $3 {(x - y)}^{2} - 6 {(x - y)}^{2} + 2 {(x - y)}^{2}$ 的结果为．

(2)、已知 $a^{2} - 2 b = 2$ ，求 $4 a^{2} - 8 b - 9$ 的值．

(3)、【拓广探索】
已知 $a - 2 b = 4 ， b - c = - 5 ， 3 c + d = 10$ ，求 $(a + 3 c) - (2 b + c) + (b + d)$ 的值．

查看试题解析
12. 阅读理解学习：
【阅读材料】一个含有多个字母的代数式中，如果任意交换两个字母的位置，代数式的值都不变，这样的代数式叫做对称式．例如：代数式 $a b c$ 中任意两个字母交换位置，可得到代数 $b a c, a c b, c b a$ ，因为 $a b c = b a c = a c b = c b a$ ，所以 $a b c$ 是对称式；而代数式 $a - b$ 中字母 $a, b$ 交换位谓，得到代数式 $b - a$ ，因为 $a - b$ 与 $b - a$ 不一定相等，所以 $a - b$ 不是对称式．
【理解判断】下列四个代数式中，是对称式的是_______________（填序号即可）；
① $a^{2} + b^{2}$ ；② $a^{2} b$ ；③ $\frac{b}{a}$ ；④ $a + b + c$
【能力提升】
（1）请直接写出一个只含有字母 $x, y$ 的单项式，使该单项式是对称式，且次数为8次；
（2）已知 $A = 2 a^{3} b^{2} - 3 b^{2} c^{2} + \frac{1}{4} a c^{2}, B = 3 a^{3} b^{2} - 4 b^{2} c^{2}$ ，求 $4 A - 3 B$ ，并直接判断所得结果是否为对称式．

查看试题解析