整式的加减运算—北师大版数学七（上）知识点训练

试卷更新日期：2024-11-10 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 化简 $\frac{1}{2}$ (8x-2)-3(x+1)的结果是（）

A、x+1 B、3x-1 C、7x+1 D、x-4

查看试题解析
2. 一个多项式与5a²+2a﹣1的和是6a²﹣5a+3，则这个多项式是（　　）

A、a²﹣7a+4 B、a²﹣3a+2 C、a²﹣7a+2 D、a²﹣3a+4

查看试题解析
3. 一个代数式减去-2x得 $- 2 x^{2} - 2 x + 1,$ 则这个代数式为 ( )

A、 $- x^{2} + 1$ B、 $- 2 x^{2} - 4 x + 1$ C、 $- 2 x^{2} + 1$ D、 $- 2 x^{2} - 4 x$

查看试题解析
4. 若A和B都是五次多项式，则A+B一定是（　　）

A、十次多项式 B、五次多项式 C、数次不高于5的整式 D、次数不低于5次的多项式

查看试题解析
5. 如果a和-4b互为相反数，那么多项式2(-b-2a+10)+3(a+2b-3)的值是（）

A、11 B、29 C、0 D、9

查看试题解析
6. 已知 $M = 4 x^{2} - 3 x - 2 ， N = 6 x^{2} - 3 x + 6$ ，则 $M$ 与 $N$ 的大小关系是（）

A、 $M < N$ B、 $M > N$ C、 $M = N$ D、以上都有可能

查看试题解析
7. 要使多项式 $m x^{2} - (5 - x + x^{2})$ 化简后不含x的二次项，则m等于（）

A、0 B、1 C、 $- 1$ D、 $- 5$

查看试题解析
8. 多项式与 $m^{2} + m - 2$ 的和是 $m^{2} - 2 m$ ．

查看试题解析
9. 若a-2b＝2，则1+3a-6b的值是．

查看试题解析
10. 化简：

(1)、 $2 x^{2} + 1 - 3 x + 7 - 2 x^{2} + 5 x$ ；

(2)、 $4 (x^{2} - x y + 6) - 3 (2 x^{2} + x y)$

查看试题解析
11. 已知 $A = x y^{2} + 6 x^{2} y$ ， $B = 3 x^{2} y - x y^{2} + 1$ ，化简： $(A + 3 B) - (B + 2 A)$ （结果用含 $x$ ， $y$ 的式子表示）．

查看试题解析
12. 已知 $A = 3 x^{2} + 2 x y - 10 y - 1$ ， $B = x^{2} - x y$ ．

(1)、计算： $A - 3 B$ ；

(2)、若 $A - 3 B$ 的值与 $y$ 的取值无关，求 $x$ 的值．

查看试题解析

二、能力提升

13. 已知无论x，y取什么值，多项式 $(2 x^{2} - m y +$ $12) - (n x^{2} + 3 y - 6)$ 的值都等于定值 18，则m+n等于 ( )

A、5 B、-5 C、1 D、-1

查看试题解析
14. 在日历上，某些数满足一定的规律．下图是某年8月份的日历，任意选择其中所示的含4个数字的方框部分，设右上角的数字为 $a$ ，则下列叙述中正确的是（）
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

A、左上角的数字为 $a + 1$ B、左下角的数字为 $a + 7$ C、右下角的数字为 $a + 8$ D、方框中4个位置的数相加，结果是4的倍数

查看试题解析
15. 若多项式 $2 x^{3} - 8 x^{2} + x - 1$ 与多项式 $3 x^{2} + 2 m x^{2} - 5 x + 3$ 相加后不含二次项，则m的值为．

查看试题解析
16. 图所示是一个正方体的表面展开图，且相对两个面表示的整式的和都相等.如果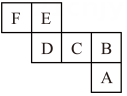 $A = a^{3} + \frac{1}{5} a^{2} b + 3 ， B = \frac{1}{2} a^{2} b - 3 ， C = a^{3} - 1 ， D = - \frac{1}{2} (a^{2} b - 6)$ ，那么 $F$ 所代表的整式是.

查看试题解析
17. 某同学做一道数学题：已知两个多项式 $A$ ， $B$ ，计算 $2 A + B$ ．他误将 $2 A + B$ 看成 $A + 2 B$ ，得到的结果是 $9 x^{2} - 2 x + 7$ ，若已知 $B = x^{2} + 3 x - 2$ ，求 $2 A + B$ 的正确答案．

查看试题解析
18. （1）有这样一道题：“当 $a = 3, b = - \frac{1}{2}$ ，求代数式：7a³﹣6a³b+3a²b+3a³+6a³b﹣3a²b﹣10a³+3的值”；小明细算了一下，提出题中所给的条件 $a = 3, b = - \frac{1}{2}$ 是多余的，请你认真计算一下，认为他的说法是否有道理？
（2）小红做了一道数学题：“已知两个多项式为A、B，其中B=4a²﹣5a﹣6，求A+B的值．”粗心的小红误将“A+B”看成“A﹣B”，结果求出的答案是10a﹣7a²+12，请你帮助小红求出正确的A+B的结果．

查看试题解析
19. 如图①，现有三种边长分别为3，2，1的正方形卡片，分别记为Ⅰ，Ⅱ，Ⅲ．还有一个长为a，宽为b的长方形．

(1)、如图②，将Ⅰ放入长方形中，试用含a，b的代数式表示阴影部分的面积，并求当 $a = 4.5$ ， $b = 4$ 时阴影部分的面积．

(2)、将Ⅰ，Ⅱ两张卡片按图③的方式，放置在长方形中，试用含a，b的代数式表示阴影部分的面积，并求当 $a = 4.5$ ， $b = 4$ 时阴影部分的面积．

(3)、将Ⅰ，Ⅱ，Ⅲ三张卡片按图④的方式，放置在长方形中，求右上角阴影部分与左下角阴影部分周长的差．

查看试题解析

三、拓展创新

20. 对于多项式： $x + 1$ ， $2 x - 2$ ， $3 x + 4$ ， $4 x - 5$ 我们用任意两个多项式求差后所得的结果，再与剩余两个多项式的差相加求和，并算出结果，称之为“差之和操作”
例如： $(x + 1) - (2 x - 2) = - x + 3$ ， $(3 x + 4) - (4 x - 5) = - x + 9$ ； $(- x + 3) + (- x + 9) = - 2 x + 12$
给出下列说法：
①只存在一种“差之和操作”，使其结果为单项式；
②至少存在一种“差之和操作”，使其结果为 $- 2 x + 12$ ；
③所有的“差之和操作”只共有4种不同的结果．
以上说法中正确的是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
21. 定义：若a+b＝2，则称a与b是关于1的平衡数．
（1）3与________是关于1的平衡数，5﹣x与________是关于1的平衡数．（用含x的代数式表示）
（2）若a＝2x²﹣3(x²+x)+4，b＝2x﹣[3x﹣(4x+x²)﹣2]，判断a与b是否是关于1的平衡数，并说明理由．

查看试题解析

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31