乘法公式—人教版数学八年级上册知识点训练
试卷更新日期:2024-11-05 类型:复习试卷
一、夯实基础
-
1. 如图,从边长为m的大正方形中剪掉一个边长为n的小正方形,将阴影部分沿虚线剪开拼成右边的长方形,根据图形的变化过程,写出一个正确的等式是( )
 A、 B、 C、 D、2. 已知是完全平方式,则常数 .
A、 B、 C、 D、2. 已知是完全平方式,则常数 .二、能力提升
-
3. 若 , , 则的值为( )A、 B、 C、 D、4. 已知 , 则的值是( )A、 B、 C、 D、5. 我们可以利用图形中的面积关系来解释很多代数恒等式.给出以下4组图形及相应的代数恒等式:
①
 ②
②
③
 ④
④
其中,图形的面积关系能正确解释相应的代数恒等式的有( )
A、1个 B、2个 C、3个 D、4个6. 从边长为a的大正方形纸板正中央挖去一个边长为b的小正方形后,将其裁成四个大小和形状完全相同的四边形(如图1),然后拼成一个平行四边形(如图2),那么通过计算两个图形阴影部分的面积,可以验证成立的等式为( ) A、 B、 C、 D、7. 阅读理解:
A、 B、 C、 D、7. 阅读理解:例:若 , 求和的值.
解:
即
,
,
我们把以上方法称为“拆项法”
请用拆项法解决问题:
(1)、 , 求的值;(2)、已知a,b,c是的三边长,满足 , c是中的最短边长,且c为整数,那么c的值可能是______(有几个写几个)三、拓展创新
-
8. 阅读下列文字:我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如,由图可以得到 . 请解答下列问题:
 (1)、小明同学打算用如图的x张边长为a的正方形纸片A和y张边长为b的正方形纸片 B,z张相邻两边长分别为a、b的长方形纸片 C拼出一个面积为的长方形,那么他总共需要 张纸片A、 张纸片B、 张纸片 C;(2)、写出图中所表示的数学等式 ;(3)、利用(2)中所得到的结论,解决下面的问题:已知求的值.9. 【阅读理解】
(1)、小明同学打算用如图的x张边长为a的正方形纸片A和y张边长为b的正方形纸片 B,z张相邻两边长分别为a、b的长方形纸片 C拼出一个面积为的长方形,那么他总共需要 张纸片A、 张纸片B、 张纸片 C;(2)、写出图中所表示的数学等式 ;(3)、利用(2)中所得到的结论,解决下面的问题:已知求的值.9. 【阅读理解】若满足 , 求的值.
解:设 , 则 ,
,
我们把这种方法叫做换元法.利用换元法达到简化方程的目的,体现了转化的数学思想.
【解决问题】
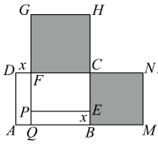 (1)、若满足 , 则 ;(2)、若满足 , 求的值;(3)、如图,在长方形中, , 点是边上的点, , 且 , 分别以为边在长方形外侧作正方形和 , 若长方形的面积为 , 求图中阴影部分的面积和.10. 阅读理解题:
(1)、若满足 , 则 ;(2)、若满足 , 求的值;(3)、如图,在长方形中, , 点是边上的点, , 且 , 分别以为边在长方形外侧作正方形和 , 若长方形的面积为 , 求图中阴影部分的面积和.10. 阅读理解题:定义:如果一个数的平方等于 , 记为 , 这个数叫做虚数单位那么形如为实数的数就叫做复数,叫这个复数的实部,叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算: .
;
.
(1)、填空: , ;(2)、计算:;;(3)、若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知: , 为实数 , 求的值;
(4)、试一试:请你参照这一知识点,将为实数因式分解成两个复数的积.