人教版数学九年级全册知识点训练营——图形的相似

试卷更新日期：2024-11-05 类型：复习试卷

进入出卷网下载

一、夯实基础

二、能力提升

1.
已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，则AD=（　　）

A、 $\frac{1 - \sqrt{5}}{2}$ B、 $\frac{1 + \sqrt{5}}{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
2. 将一个矩形纸片ABCD沿AD和BC的中点的连线对折，要使矩形AEFB与原矩形相似，则原矩形的长和宽的比应为（　　）

A、 $2 ： 1$ B、 $\sqrt{3} ： 1$ C、 $\sqrt{2} ： 1$ D、 $1 ： 1$

查看试题解析
3.
如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的 $\frac{1}{4}$ ，那么点B′的坐标是（　　）

A、（﹣2，3） B、（2，﹣3） C、（3，﹣2）或（﹣2，3） D、（﹣2，3）或（2，﹣3）

查看试题解析
4. 已知四边形ABCD与四边形A'B'C′D'相似，边AB与边A'B'是对应边，S_{四边形ABCD}：S_{四边形A'B′C′D'}＝2：4，AB＝2，则A'B'＝.

查看试题解析
5. 下列说法：①位似图形都相似；②两个等腰三角形一定相似；③任意两个菱形一定相似；④任意两个含30°角的直角三角形一定相似；⑤两个相似多边形的面积比为4：9，则周长比为16：81；⑥若一个三角形的三边分别比另一个三角形的三边长2cm，则这两个三角形一定相似．其中正确的说法有（填写序号）．

查看试题解析
6.
如图，菱形ABCD和菱形ECGF的边长分别为2和3，∠A＝120°，则图中阴影部分的面积是多少？

查看试题解析
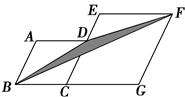
7.
如图，在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP=a．

（1）当点P在线段BC上时（点P与点B，C都不重合），试用含a的代数式表示CE；
（2）当a=3时，连结DF，试判断四边形APFD的形状，并说明理由；
（3）当tan∠PAE= $\frac{1}{2}$ 时，求a的值．

查看试题解析
8. 如图是由边长相等的小正方形组成的网格，以下各图中点A、B、C、D都在格点上.

(1)、在图1中，PC：PB＝.

(2)、利用网格和无刻度的直尺作图，保留痕迹，不写作法.
①如图2，在AB上找点P，使得AP：PB＝1：3；

②如图3，在△ABC中内找一点G，连接GA、GB、GC，将△ABC分成面积相等的三部分；

③如图4，在△ABC中，AB与网格线的交点为D，画点E，使DE⊥AC.

查看试题解析
9. 如图，在△ABC中，AC＝4.

(1)、在AC上求作一点D，连接BD，使得△ABD∽△ACB；（要求：尺规作图，不写作法，保留作图痕迹）

(2)、点M，N分别是BD、BC中点，若AD＝1，求 $\frac{A M}{A N}$ 的值.

查看试题解析
10. 如图， $▱ A B C D$ 中， $∠ B A D$ 的平分线交 $B C$ 于点 $E$ ， $∠ A B C$ 的平分线交 $A D$ 于点 $F$ .

(1)、求证： $▱ A B E F$ 是菱形：

(2)、若 $▱ A B C D ∽ ▱ F D C E$ ，则 $\frac{B C}{C D}$ 的值为.

查看试题解析

三、拓展创新

11. 下列说法不一定正确的是（　　）

A、所有的等边三角形都相似 B、所有的等腰直角三角形都相似 C、所有的菱形都相似 D、所有的正方形都相似

查看试题解析
12. 如图，抛物线 $y = a x_{}^{2} + b x + 4 (a \neq 0)$ 与x轴交于点A（ $- 1$ ， 0）和点B（4，0），与y轴交于点C ，顶点为D ，连接AC ， BC ， BC与抛物线的对称轴l交于点E

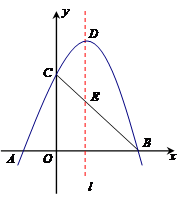(1)、求抛物线的表达式；

(2)、点P是第一象限内抛物线上的动点，连接PB ， PC ，若 $S_{Δ P B C}^{} = \frac{3}{5} S_{Δ A B C}^{}$ ，求点P的坐标；

(3)、点N是对称轴l右侧抛物线上的动点，在射线ED上是否存在点M ，使得以点M ， N ， E为顶点的三角形与 $Δ O B C$ 相似？若存在，直接写出点M的坐标；若不存在，说明理由。

查看试题解析
13. 如图，已知矩形 $O A B C$ 的顶点 $B (- 8 ， 6)$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，点 $A$ 在 $x$ 轴上，点 $C$ 在 $y$ 轴上，点 $P$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，其横坐标为 $a (a < - 8)$ ，过点 $P$ 作 $P E ⊥ x$ 轴于点 $E$ ， $P F ⊥ y$ 轴于点 $F$ ，交 $A B$ 于点 $G$ ．

(1)、求反比例函数的解析式；

(2)、若四边形 $P E A G$ 为正方形，求点 $P$ 的坐标；

(3)、连接 $O P$ 交 $A B$ 于点 $M$ ，若 $B M ： M A = 3 ： 2$ ，求四边形 $P E A M$ 与四边形 $B M O C$ 的面积比．

查看试题解析