浙教版数学八上第5章 一次函数 三阶单元测试卷
试卷更新日期:2024-11-03 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 直线与直线在同一平面直角坐标系中的图象如图所示,则不等式的解为( )
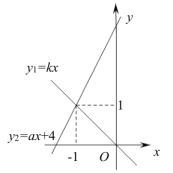 A、 B、 C、 D、2. 对于一次函数 , 结论如下:
A、 B、 C、 D、2. 对于一次函数 , 结论如下:①函数的图象不经过第三象限;②函数的图象与x轴的交点坐标是
③将函数的图象向下平移2个单位长度可以得到的图象;
④若两点 , 在该函数图象上,则 . 其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个3. 已知一次函数与( , 为常数,且),则它们在同一平面直角坐标系内的图象可能为( )A、 B、
B、 C、
C、 D、
D、 4. 在同一直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( )
4. 在同一直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( ) A、随的增大而减小 B、 C、方程组的解为 D、当时,5. 小明在一条公路上开车从A地出发行驶至B地,他行驶的行程y(千米)随时间x(时)变化的图象(全程)如图所示.则下列说法中,错误的是( )
A、随的增大而减小 B、 C、方程组的解为 D、当时,5. 小明在一条公路上开车从A地出发行驶至B地,他行驶的行程y(千米)随时间x(时)变化的图象(全程)如图所示.则下列说法中,错误的是( ) A、第1小时小明行驶了21千米 B、在行驶的前小时内,小明行驶的平均速度是42千米/小时 C、在小时内,小明行驶的速度相比前小时变慢 D、A地到B地的距离为40千米6. 在平面直角坐标系中,点 , 在函数的图像上,则( )A、 B、 C、 D、以上都有可能7. 如图,直线 与 相交于点 ,点 的横坐标为 ,则关于 的不等式 的解集在数轴上表示正确的是( )
A、第1小时小明行驶了21千米 B、在行驶的前小时内,小明行驶的平均速度是42千米/小时 C、在小时内,小明行驶的速度相比前小时变慢 D、A地到B地的距离为40千米6. 在平面直角坐标系中,点 , 在函数的图像上,则( )A、 B、 C、 D、以上都有可能7. 如图,直线 与 相交于点 ,点 的横坐标为 ,则关于 的不等式 的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,点G是的中点,点H在上,动点P以每秒的速度沿图1的边线运动,运动路径为: , 相应的的面积关于运动时间的函数图象如图2,若 , 则下列六个结论中正确的个数有( )
8. 如图,点G是的中点,点H在上,动点P以每秒的速度沿图1的边线运动,运动路径为: , 相应的的面积关于运动时间的函数图象如图2,若 , 则下列六个结论中正确的个数有( )
①图1中的长是;
②图2中的M点表示第4秒时y的值为;
③图1中的长是;
④图1中的长是;
⑤图2中的Q点表示第8秒时y的值为33;
⑥图2中的N点表示第12秒时y的值为 .
A、3个 B、4个 C、5个 D、6个9. 若实数x,y满足|x|+4|y|=1,则m=y-4x的最大值是( )A、1 B、2 C、3 D、410. 如图,在同一平面直角坐标系中,一次函数与 , 小聪根据图象得到如下结论:①;②关于x,y的方程组的解为;③关于x的方程的解为;④关于x的不等式的解集是 .
其中结论正确的个数是( )
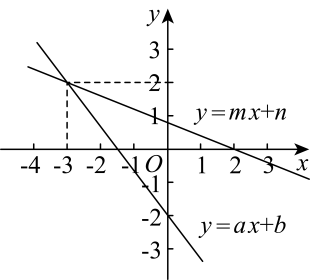 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(本题有6小题,每小题4分,共24分)
-
11. 若点和点在一次函数的图象上,则 .12. 在平面直角坐标系中,若将一次函数的图象向下平移3个单位后经过原点,则m的值为 .13. 甲、乙两船沿直线航道匀速航行.甲船从起点A出发,同时乙船从航道中途的点B出发,向终点C航行.设t小时后甲、乙两船与B处的距离分别为 , 则与t的函数关系如图.下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是 . 其中正确的说法的是 .
 14. 如图 , 在平面直角坐标系中,等腰在第一象限,且 轴,直线从原点出发沿轴正方向平移,在平移过程中,直线被截得的线段长度与直线在轴上平移的距离的函数图象如图所示,那么的面积为
14. 如图 , 在平面直角坐标系中,等腰在第一象限,且 轴,直线从原点出发沿轴正方向平移,在平移过程中,直线被截得的线段长度与直线在轴上平移的距离的函数图象如图所示,那么的面积为 15. 一次函数与函数的图象恰好有两个交点,则实数k的取值范围是 .16. 在平面直角坐标系中,为坐标原点,将函数(为常数)的图象位于轴下方的部分沿轴翻折至其上方后,所得的折线是函数(b为常数)的图象.若函数(为常数)与直线有交点A、B,现给出以下结论,其中正确结论的序号是 .
15. 一次函数与函数的图象恰好有两个交点,则实数k的取值范围是 .16. 在平面直角坐标系中,为坐标原点,将函数(为常数)的图象位于轴下方的部分沿轴翻折至其上方后,所得的折线是函数(b为常数)的图象.若函数(为常数)与直线有交点A、B,现给出以下结论,其中正确结论的序号是 .①的面积总为;
②若函数(为常数)图象在直线下方的点的横坐标x满足 , 则b的取值范围为;
③若 , 则的解集为;
④当 , 若正比例函数与(为常数)的图象只有一个公共点,则 .
三、解答题(本题共8小题,第17题6分,第18题6分,第19题8分,第20题6分,第21题10分,第22题10分,第23题10分,第24题10分,共66分)
-
17. 在平面直角坐标系中,直线:与直线交于点 , 直线与轴交于点 .
 (1)、求点的坐标(用含的代数式表示);(2)、横、纵坐标都是整数的点叫做整点.将内(不含边界)的整点个数记为 ,
(1)、求点的坐标(用含的代数式表示);(2)、横、纵坐标都是整数的点叫做整点.将内(不含边界)的整点个数记为 ,①当时,结合函数图象,直接写出的值;
②若 , 直接写出的取值范围.
18. 年月日至日第二届湖南旅游发展大会在郴州市举行“当好东道主,热情迎嘉宾”,郴州某知名小吃店计划购买 , 两种食材制作小吃,已知购买千克种食材和千克种食材共需元,购买千克种食材和千克种食材共需元.
(1)、求 , 两种食材的单价;(2)、该小吃店计划购买两种食材共千克,其中购买种食材千克数不少于种食材千克数的倍,当 , 两种食材分别购买多少千克时,总费用最少?并求出最少总费用.19. 如图1, 已知∠A=∠B, AC=6cm, AB=20cm, 点P在线段AB上由点B向点A运动,点 P 的运动速度 v(cm/s)与运动时间t(s)之间的关系如图2所示. (1)、 点 P的运动速度为 cm/s;(2)、当点P运动t秒时,求线段AP的长(用含t的代数式表示);(3)、点Q在射线BM上由点B 向点M运动,与点P同时出发,当点 P 运动结束时,点Q运动随之结束. 当点Q的速度是多少时,△ACP与△BPQ全等?20. 根据以下信息,探索完成任务:
(1)、 点 P的运动速度为 cm/s;(2)、当点P运动t秒时,求线段AP的长(用含t的代数式表示);(3)、点Q在射线BM上由点B 向点M运动,与点P同时出发,当点 P 运动结束时,点Q运动随之结束. 当点Q的速度是多少时,△ACP与△BPQ全等?20. 根据以下信息,探索完成任务:如何选择合适的话费套餐
素材1
中国移动A套餐:月租费为58元/月,套餐内每月可拨打国内电话150分钟,超出套餐部分拨打国内电话0.19元/分钟.
素材2
中国移动B套餐:月租费为88元/月,套餐内每月可拨打国内电话350分钟,超出套餐部分拨打国内电话0.19元/分钟.
素材3
中国移动推出的A,B两种套餐都在全国范围内接听免费,含来电显示.
套餐收费说明:如A套餐计费方法中,若拨打国内电话时长小于等于150分钟,则只收月租费58元/月;若拨打国内电话时长为180分钟,则该月计费为58+(180-150)×0.19=63.7元.
任务一
某用户选择中国移动B套餐:
若该月拨打国内电话时长为200分钟,则该用户的月缴费为 ▲ 元;
若该月拨打国内电话时长为380分钟,则该用户的月缴费为 ▲ 元.
任务二
若选择A套餐计费方法,设某用户一个月的拨打国内电话时长为x分钟(x>150),该月话费为y1元,则y1与x的关系式是 ▲ ;若选择B套餐计费方法,设某用户一个月的拨打国内电话时长为x分钟(x>350),该月话费为y2元,则y2与x的关系式是 ▲ .
任务三
若某用户某月拨打国内电话总时长为250分钟,你认为他应该选择上述两种套餐中的哪一种较为合算?请说明你的理由.
21. 本学期,我们学习了“一元一次不等式与一次函数”,请利用所学知识来解决下面的问题:在函数中, 下表是y与x的几组对应值.
x
…
0
1
2
3
y
...
7
m
3
1
n
1
3
(1)、m= , n= ;(2)、在下面给出的平面直角坐标系中,画出这个函数的图象; (3)、根据图象,下列关于该函数性质的说法中正确的是 . (填序号)
(3)、根据图象,下列关于该函数性质的说法中正确的是 . (填序号)①该函数图象是轴对称图形,对称轴为直线 .
②当时, y随x的增大而增大,当时,y随x的增大而减小.
③该函数在自变量的取值范围内有最小值,当时有最小值 .
(4)、根据图象, 直接写出不等式:的解集 .22. 如图,在平面直角坐标系中,已知直线:分别与轴,轴交于 , 两点,与直线:交于点 . (1)、求的值及直线的函数解析式;(2)、当时,满足不等式 , 求的取值范围;(3)、若直线:与的边有两个公共点,求的取值范围.23. 甲、乙两位同学从学校出发沿同一条绿道到相距学校 的图书馆去看书,甲步行,乙骑自行车.图1中 , 分别表示甲、乙离开学校的路程 与甲行走的时间 之间的函数图象.
(1)、求的值及直线的函数解析式;(2)、当时,满足不等式 , 求的取值范围;(3)、若直线:与的边有两个公共点,求的取值范围.23. 甲、乙两位同学从学校出发沿同一条绿道到相距学校 的图书馆去看书,甲步行,乙骑自行车.图1中 , 分别表示甲、乙离开学校的路程 与甲行走的时间 之间的函数图象. (1)、求线段 所在直线的函数表达式;(2)、设 表示甲、乙两人之间的路程,在图2中补全d关于x的函数图象;(标注必要的数据)(3)、当x在什么范围时,甲、乙两人之间的路程至少为 .24. 如图 , 在平面直角坐标系中,直线:与轴交于点 , 与轴交于点 , 直线与轴交于点 , 与轴交于点, , .
(1)、求线段 所在直线的函数表达式;(2)、设 表示甲、乙两人之间的路程,在图2中补全d关于x的函数图象;(标注必要的数据)(3)、当x在什么范围时,甲、乙两人之间的路程至少为 .24. 如图 , 在平面直角坐标系中,直线:与轴交于点 , 与轴交于点 , 直线与轴交于点 , 与轴交于点, , .
(1)、求直线的解析式;(2)、连接 , 点为直线上一动点,若有 , 求点的坐标;(3)、点为直线上一点,点为轴上一点,若 , , 三点构成以为直角边的等腰直角三角形,求点的坐标.