浙教版数学八上第5章 一次函数 二阶单元测试卷
试卷更新日期:2024-11-03 类型:单元试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 若点P在一次函数y=-x+4的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 一次函数y=x+2的图象与y轴的交点坐标为( )A、(0,2) B、(0,-2) C、(2,0) D、(-2,0)3. 下列各曲线中,不能表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若函数y=(k﹣3)x+k2﹣9是正比例函数,则( )A、k≠3 B、k=±3 C、k=3 D、k=﹣35. 对于一次函数 , 下列说法错误的是( )A、随的增大而减小 B、图象与轴交点为 C、图象经过第一、二、四象限 D、图象经过点6. 河南是中原粮仓,粮食的水分含量是评价粮食品质的重要指标,粮食水分检测对粮食的收购、运输、储存等都具有十分重要的意义.其中,电阻式粮食水分测量仪的内部电路如图甲所示,将粮食放在湿敏电阻上,使的阻值发生变化,其阻值随粮食水分含量的变化关系如图乙所示.观察图象,下列说法不正确的是( )
4. 若函数y=(k﹣3)x+k2﹣9是正比例函数,则( )A、k≠3 B、k=±3 C、k=3 D、k=﹣35. 对于一次函数 , 下列说法错误的是( )A、随的增大而减小 B、图象与轴交点为 C、图象经过第一、二、四象限 D、图象经过点6. 河南是中原粮仓,粮食的水分含量是评价粮食品质的重要指标,粮食水分检测对粮食的收购、运输、储存等都具有十分重要的意义.其中,电阻式粮食水分测量仪的内部电路如图甲所示,将粮食放在湿敏电阻上,使的阻值发生变化,其阻值随粮食水分含量的变化关系如图乙所示.观察图象,下列说法不正确的是( ) A、当没有粮食放置时,的阻值为 B、粮食水分含量为时,的阻值为 C、的阻值随着粮食水分含量的增大而减小 D、该装置能检测的粮食水分含量的最大值是7. 如图,直线y=﹣x+b和y=kx﹣3交于点P , 根据图象可知kx﹣3<﹣x+b的解集为( )
A、当没有粮食放置时,的阻值为 B、粮食水分含量为时,的阻值为 C、的阻值随着粮食水分含量的增大而减小 D、该装置能检测的粮食水分含量的最大值是7. 如图,直线y=﹣x+b和y=kx﹣3交于点P , 根据图象可知kx﹣3<﹣x+b的解集为( ) A、x>1 B、x<1 C、0<x<1 D、﹣2<x<18. 如图1所示为某景区游览路线及方向,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程与时间的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.
A、x>1 B、x<1 C、0<x<1 D、﹣2<x<18. 如图1所示为某景区游览路线及方向,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程与时间的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.则路线①③⑥⑦⑧各路段路程之和为
 A、4200米 B、4800米 C、5200米 D、5400米9. 一次函数y=(m-2)x+2-m和y=x+m在同一平面直角坐标系中的图象可能是( )A、
A、4200米 B、4800米 C、5200米 D、5400米9. 一次函数y=(m-2)x+2-m和y=x+m在同一平面直角坐标系中的图象可能是( )A、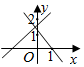 B、
B、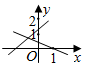 C、
C、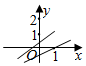 D、
D、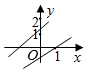 10. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A , 与y轴交于点B , 点P在线段上,轴于点C , 则周长的最小值为( )
10. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A , 与y轴交于点B , 点P在线段上,轴于点C , 则周长的最小值为( )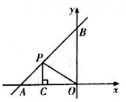 A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 已知正比例函数的图象过点 , 则该函数的解析式为 .12. 在平面直角坐标系xOy中,若直线y=2x+3向下平移n个单位长度后,与直线y=﹣x+2的交点在第一象限,则n的取值范围是 .13. 如图,平面直角坐标系中,经过点的直线与直线相交于点 , 则不等式的解集为 .
 14. 在平面直角坐标系中,已知直线l:过点 , 且与坐标轴交于点 , 则当的面积为2,且直线与轴不平行时,直线的表达式为 .
14. 在平面直角坐标系中,已知直线l:过点 , 且与坐标轴交于点 , 则当的面积为2,且直线与轴不平行时,直线的表达式为 . 15. 如图,在平面直角坐标系中,直线:与直线:交于点 , 直线与轴交于点 , 直线:过点 , 点是横轴上任意一点,满足:是等腰三角形的点坐标是 .
15. 如图,在平面直角坐标系中,直线:与直线:交于点 , 直线与轴交于点 , 直线:过点 , 点是横轴上任意一点,满足:是等腰三角形的点坐标是 .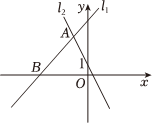 16. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .
16. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .三、解答题(本题共8小题,第17题6分,第18题6分,第19题6分,第20题6分,第21题14分,第22题6分,第23题10分,第24题12分,共66分)
-
17. 在平面直角坐标系中,一次函数的图象与函数的图象平行,且过点 .(1)、求这个一次函数的表达式;(2)、当时,对于的每一个值,函数的值都大于函数的值,直接写出的取值范围.18. 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后按原路返回.设汽车从甲地出发(h)时,汽车离甲地的路程为(km),与的函数关系如图所示.根据图象信息,解答下列问题:
 (1)、这辆汽车的往、返速度是否相同?请说明理由;(2)、求这辆汽车从甲地出发几小时时离乙地的路程为60km.19. 如图,一次函数y1=2x﹣2的图象与y轴交于点A , 一次函数y2的图象与y轴交于点B(0,6),点C为两函数图象的交点,且点C的横坐标为2.
(1)、这辆汽车的往、返速度是否相同?请说明理由;(2)、求这辆汽车从甲地出发几小时时离乙地的路程为60km.19. 如图,一次函数y1=2x﹣2的图象与y轴交于点A , 一次函数y2的图象与y轴交于点B(0,6),点C为两函数图象的交点,且点C的横坐标为2. (1)、求一次函数y2的函数解析式;(2)、求△ABC的面积;20. 已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)、求一次函数y2的函数解析式;(2)、求△ABC的面积;20. 已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?
21. 综合与实践同学,还记得学习研究一次函数的路径吗?请结合一次函数的学习经验探究函数的图象.
 (1)、列表:
(1)、列表:x
…
-4
-3
-2
-1
0
1
2
…
y
…
3
m
-1
-3
-1
n
3
…
表格中 , ;
(2)、在下面的平面直角坐标系中画出该函数的图象;(3)、观察(2)中所画函数的图象,写出关于该函数的两条结论.结论1: ▲ ;
结论2: ▲ ;
(4)、写出关于的方程的解,并简单说明此方程的解是如何得到的.22. 综合与实践某班同学分三个小组进行“板凳中的数学”的项目式学习研究.第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.

【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为x mm , 凳面的宽度为y mm , 记录如下:
以对称轴为基准向两边各取相同的长度x/mm
16.5
19.8
23.1
26.4
29.7
凳面的宽度y/mm
115.5
132
148.5
165
181.5
【分析数据】
如图③,小组根据表中x , y的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1)、观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,求出这条直线所对应的函数解析式;如果不在同一条直线上,说明理由.(2)、当凳面宽度为213mm时,以对称轴为基准向两边各取相同的长度是多少?23. 小明和小丽在跑步机上慢跑锻炼.小明先跑,10分钟后小丽才开始跑,小丽跑步时中间休息了两次.跑步机上C档比B档快40米/分、B档比A档快40米/分.小明与小丽的跑步相关信息如表所示,跑步累计里程s(米)与小明跑步时间t(分)的函数关系如图所示.时间
里程分段
速度档
跑步里程
小明
不分段
A档
4000米
小丽
第一段
B档
1800米
第一次休息
第二段
B档
1200米
第二次休息
第三段
C档
1600米
 (1)、求A,B,C各档速度(单位:米/分);(2)、求小丽两次休息时间的总和(单位:分);(3)、小丽第二次休息后,在a分钟时两人跑步累计里程相等,求a的值.24. 如图,在平面直角坐标系中,直线 : 的图象经过点 ,且与 轴交于点 ,与直线 : 交于点A , 点A的横坐标为 .
(1)、求A,B,C各档速度(单位:米/分);(2)、求小丽两次休息时间的总和(单位:分);(3)、小丽第二次休息后,在a分钟时两人跑步累计里程相等,求a的值.24. 如图,在平面直角坐标系中,直线 : 的图象经过点 ,且与 轴交于点 ,与直线 : 交于点A , 点A的横坐标为 . (1)、求直线 的解析式;(2)、直接写出关于 的不等式 的解集;(3)、若 是 轴上的点,且 ,求点 的坐标.
(1)、求直线 的解析式;(2)、直接写出关于 的不等式 的解集;(3)、若 是 轴上的点,且 ,求点 的坐标.