浙教版数学八上第5章一次函数一阶单元测试卷

试卷更新日期：2024-11-03 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 下列函数中，y是x的正比例函数的是(　　)

A、 $y = 2 x + 1$ B、 $y = 3 x^{2}$ C、 $y = x$ D、 $y = \frac{1}{x}$

查看试题解析
2. 如图所示，在同一平面直角坐标系内，直线 $l_{1} : y = k x + b$ 与直线 $l_{2} : y = m x + n$ 分别与 $x$ 轴交于点 $(- 2, 0)$ 与 $(5, 0)$ ，则不等式组 $\{\begin{array}{l} k x + b < 0 \\ m x + n > 0 \end{array}$ 的解为（）

A、 $x < - 2$ B、 $x > 5$ C、 $- 2 < x < 5$ D、无解

查看试题解析
3. 下列函数中，一次函数的是（）

A、 $y = 3 x^{4}$ B、 $y = 3 x$ C、 $y = \frac{3}{x}$ D、 $y = k x - 3$ （ $k$ 为常数）

查看试题解析
4. 选项中的曲线不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
5. 若一次函数 $y = (3 - k) x - k$ 的图象经过第二、三、四象限，则 $k$ 的取值范围是（）

A、 $k > 3$ B、 $0 < k \leq 3$ C、 $0 \leq k < 3$ D、 $0 < k < 3$

查看试题解析
6. 已知函数 $y = (2 m + 1) x + m - 3$ ，若函数图象经过原点，则 $m$ 的值是（　　）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
7. 定义：关于x的一次函数 $y = a x + b$ 与 $y = b x + a (a b \neq 0)$ 叫做一对交换函数，例如：一次函数 $y = 3 x + 4$ 与 $y = 4 x + 3$ 就是一对交换函数．现有一次函数 $y = 2 x - b$ ，当 $b \neq - 2$ 时，这个一次函数的图象与其交换函数图象交点的横坐标（）．

A、 $- 1$ B、2 C、1 D、无法确定

查看试题解析
8. 某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离 $y$ （千米）与货车行驶时间 $x$ （小时）之间的函数图象如图所示，现有以下4个结论：①快递车从甲地到乙地的速度为100千米/时；②甲、乙两地之间的距离为120千米；③图中点 $B$ 的坐标为 $(3 \frac{3}{4}, 75)$ ；④快递车从乙地返回时的速度为90千米/时．其中正确的是（）

A、①②③ B、②④ C、①③④ D、①③

查看试题解析
9. 如图，一次函数 $y = 2 x - 3$ 的图像与 $x$ 轴相较于点A，则点A关于y轴的对称点是（）

A、 $(- \frac{3}{2} ， 0)$ B、 $(\frac{3}{2} ， 0)$ C、 $(0 ， 3)$ D、 $(0 ， - 3)$

查看试题解析
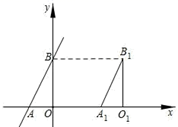
10. 如图，正方形ABCD的边长为a，动点P从点A出发，沿折线A→B→D→C→A的路径运动，回到点A时运动停止．设点P运动的路程长为x，AP长为y，则y关于x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 正比例函数 $y = k x$ 中， $y$ 的值随着 $x$ 值的增大而增大，则点 $(3, - k)$ 在第象限．

查看试题解析
12. 地表以下岩层的温度y（℃）随着所处深度x（km）的变化而变化，在某个地点y与x之间有如下关系：
x/km
1
2
3
4
y/℃
55
90
125
160
根据表格，估计地表以下岩层的温度为230℃时，岩层所处的深度为km ．

查看试题解析
13. 若 $y = k x + 2$ 的图像与 $x$ 轴 $y$ 轴所围成的三角形的面积为2，则 $k =$ ．

查看试题解析
14. 若直线 $y_{1} = \frac{1}{2} x - 2$ 与直线 $y_{2} = - \frac{1}{4} + a$ 相交于x轴同一点，则当x时， $y_{1} < y_{2}$ ．

查看试题解析
15. 一根弹簧秤原长12cm ，所挂物体的质量每增加2kg ，弹簧就伸长6cm ，则挂物体后弹簧长度y(cm)与所挂物体的质量x(kg)之间的函数表达式是．

查看试题解析
16. 在平面直角坐标系xOy中，一次函数y₁＝kx+b与y₂＝x+m的图象如图所示，若它们的交点的横坐标为2，则下列三个结论中正确的是（填写序号）．
①直线y₂＝x+m与x轴所夹锐角等于45°；②k+b＞0；③关于x的不等式kx+b＜x+m的解集是x＜2．

查看试题解析

三、解答题（本题共8小题，第17题6分，第18题8分，第19题6分，第20题8分，第21题8分，第22题14分，第23题14分，第24题8分，共66分）

17. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b$ 的图象经过点 $(- 1, 0)$ ， $(1, 2)$ ．

(1)、求这个一次函数的解析式；

(2)、当 $x > - 3$ 时，对于 $x$ 的每一个值，函数： $y = m x - 1 (m \neq 0)$ 的值小于函数 $y = k x + b$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
18. 2024深圳市梧桐山第九届毛棉杜鹃花会正式拉开帷幕，小明决定登梧桐山赏花．如图1，他以一定的速度沿路线“梧桐山北门—万花屏—好汉坡—大梧桐—深外高中站”步行游览，在每个景点他都逗留一段时间，当他到达深外高中站时，共用去 $4.6 h$ ．小明步行的路程 $s (k m)$ 与游览时间 $t (h)$ 之间的部分图象如图2所示．根据图回答下列问题：

(1)、图2中反映了两个变量之间的关系，其中自变量为          ，因变量为           ；

(2)、他从万花屏到好汉坡时行走的平均速度是                 千米/时；

(3)、小明在景点好汉坡处逗留的时间是             小时；

(4)、图2中点A表示                        ．

查看试题解析
19. 如图，在平面直角坐标中，直线 $y = - 2 x + 6$ 与x轴相交于点B，与直线 $y = 2 x$ 相交于点A．

(1)、求 $△ A O B$ 的面积；

(2)、点P为y轴上一点，当 $P A + P B$ 取最小值时，求点P的坐标，

查看试题解析
20. 小华和玲玲沿同一条笔直的马路同时从学校出发到某图书馆查阅资料，学校与图书馆的路程是5千米，小华骑共享单车，玲玲步行．当小华从原路回到学校时，玲玲刚好到达图书馆．图中折线 $O - A - B - C$ 和线段OD分别表示两人离学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系，请根据图象回答下列问题：

(1)、玲玲的速度为千米/分钟，小华返回学校的速度为千米/分钟．

(2)、小华和玲玲在出发a分钟时，两人到学校的距离相等，求a的值．

查看试题解析
21. 友谊商店笔记本电脑的售价是a元/台.最近，该商店对笔记本电脑举行促销活动，有两种优惠方案.方案一：每台按售价的九折销售；方案二：若购买不超过5台，每台按售价销售；若超过5台，超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买笔记本电脑x台.

(1)、当x=8时，选择哪种方案，可使该公司购买笔记本电脑的费用最少?最少费用是多少元?

(2)、若采用方案二购买更合算，求x的取值范围.

查看试题解析
22. 【背景】如图1是某品牌的饮水机，此饮水机有开水、温水两个按钮，图2为其信息图．
【主题】如何接到最佳温度的温水．
【素材】水杯容积：700mL．
物理知识：开水和温水混合时会发生热传递，开水放出的热量等于温水吸收的热量．即：开水体积×开水降低的温度＝温水体积×温水升高的温度．
生活经验：饮水最佳温度是35℃～38℃（包括35℃与38℃），这一温度最接近人体体温．
【操作】先从饮水机接温水x秒，再接开水，直至接满700mL的水杯为止．
（备注：接水期间不计热损失，不考虑水溢出的情况．）
【问题】

(1)、接到温水的体积是mL，接到开水的体积是mL；（用含x的代数式表示）

(2)、若所接的温水的体积不少于开水体积的2倍，则至少应接温水多少秒？

(3)、若水杯接满水后，水杯中温度是50℃，求x的值；

(4)、记水杯接满水后水杯中温度为y℃，则y关于x的关系式是；若要使杯中温度达到最佳水温，直接写出x的取值范围是．

查看试题解析
23. 如图，已知过点 $B (1,0)$ 的直线 $l_{1}$ 与直线 $l_{2}$ ： $y = 2 x + 4$ 相交于点 $P (- 1, a) .$ 且 $l_{1}$ 与 $y$ 轴相交于 $C$ 点， $l_{2}$ 与 $x$ 轴相交于 $A$ 点．

(1)、求直线 $l_{1}$ 的解析式；

(2)、求四边形 $P A O C$ 的面积；

(3)、若点 $Q$ 是 $x$ 轴上一动点，连接 $P Q$ 、 $C Q$ ，当 $△ Q P C$ 周长最小时，求点 $Q$ 坐标．

查看试题解析
24. 如图，直线AB与x轴，y轴分别交于点A和点B，点A的坐标为（−1，0），且2OA＝OB．

(1)、求直线AB解析式；

(2)、如图，将△AOB向右平移3个单位长度，得到△A₁O₁B₁ ，求线段OB₁的长；

(3)、在（2）中△AOB扫过的面积是．

查看试题解析

x/km	1	2	3	4
y/℃	55	90	125	160

浙教版数学八上第5章 一次函数 一阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题6分，第18题8分，第19题6分，第20题8分，第21题8分，第22题14分，第23题14分，第24题8分，共66分）

浙教版数学八上第5章一次函数一阶单元测试卷