浙教版数学八上第4章 图形与坐标 三阶单元测试卷
试卷更新日期：2024-11-03 类型：单元试卷
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 用方位表示物体的位置，下列表示正确的是( ).A、新星公园在学校的正南方向 B、新星公园距学校3km C、学校在新星路38号 D、学校在新星公园的正北方向3km处2. 如图，在直角坐标系中，△ABC的顶点都在方格纸的格点上.如果将△ABC先向右平移4个单位长度，再向下平移1个单位长度，得到△A1B1C1 ， 那么点A的对应点A1的坐标为( ).
A、(4，3) B、(2，4) C、(3，1) D、(2，5)3. 如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是（ ）
A、（0，0） B、（0，1） C、（0，2） D、（0，3）4. 在平面直角坐标系中，若点在第三象限，则x的取值范围是（ ）A、 B、 C、 D、5. 如图，将一片枫叶固定在正方形网格中，若点A的坐标为 ， 点C的坐标为 ， 则点B的坐标为（ ）
A、 B、 C、 D、6. 若点P关于x轴的对称点为 ， 关于y轴的对称点为 ， 则P点的坐标为（ ）A、 B、 C、 D、7. 下列说法中正确的是（ ）A、(-2，2)与(2，-2)关于x轴对称 B、平行于y轴的直线上所有点的纵坐标都相同 C、若点A(3，-1)，则点A到x轴的距离为1 D、若点Q(a，b)在x轴上，则a=08. 在平面直角坐标系xOy中，对于点P（x，y）我们把P（-y+1，x+1）叫做点P的伴随点，已知A1的伴随点为A2 ， 点A2的伴随点为A3 ， 点A3的伴随点为A4 ， 这样依次得到A1 ， A2 ， A3 ， …An ， 若点A1的坐标为（3，1），则点A2023的坐标为 （ ）A、（0，4） B、（3，1） C、（-3，1） D、（0，-2）9. 在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右、向上、向右、向下的方向依次不断移动，每次移动1m，其行走路线如图所示，第1次移动到点A1 ， 第2次移动到点A2……第n次移动到点An，则△OA2A2022的面积是（ ）
A、505m² B、 m² C、 m² D、1 009 m²二、填空题（本题有6小题，每小题4分，共24分）
-
10. 若点A（3，﹣2）与点B关于y轴对称，则点B的坐标为 ．11. 点A在平面直角坐标系第二象限，距离x轴3个单位长度，距离y轴5个单位长度，则点A的坐标是.12. 在平面直角坐标系中，线段AB的端点坐标分别为A（2，﹣1），B（1，0），将线段AB平移后，点A的对应点A'的坐标为（2，1），则点B的对应点B'的坐标为 ．13. 如下图所示，在平面直角坐标系中，点P的坐标为 ， 点Q是x轴上的一个动点，当线段的长最小时，点Q的坐标为 ．
14. 在平面直角坐标系中，对于点 ， 如果点的纵坐标满足：当时；当时.那么称点Q为点P的“关联点”.如果点的关联点Q坐标为 ， 则点P的坐标为.15. 如图，点 ， 点 ， 点 ， 点 ， 按照这样的规律下去，点的坐标为 ．
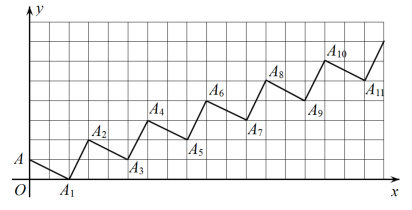
三、解答题（本题共8小题，第17题8分，第18题7分，第19题7分，第20题7分，第21题9分，第22题7分，第23题11分，第24题10分，共66分）
-
16. 已知点P(2m+4，m-1).试分别根据下列条件，求出点P的坐标.(1)、点P在y轴上.(2)、点P在x轴上.(3)、点P的纵坐标比横坐标大3.(4)、点P在过点A(2，-3)，且与x轴平行的直线上.17. 围棋，起源于中国，古代称为“弈”，是棋类鼻祖，距今已有4000多年的历史．如图是某围棋棋盘的局部，若棋盘是由边长均为1的小正方形组成的，棋盘上A、B两颗棋子的坐标分别为 ， ．
(1)、根据题意，画出相应的平面直角坐标系；(2)、分别写出C、D两颗棋子的坐标；(3)、有一颗黑色棋子E的坐标为 ， 请在图中画出黑色棋子E．18. 已知点 ， 解答下列各题：
(1)、若点在轴上，则点的坐标为；(2)、若 ， 且轴，则点的坐标为；(3)、若点在第二象限，且它到轴、轴的距离相等，求的值．
19. 如图1，在平面直角坐标系中，点A，B的坐标分别为 ， ， 且a，b满足 ， 现将线段先向上平移4个单位长度，再向右平移6个单位长度得到线段 ， 其中点A对应点为C，点B对应点为D，连接 ， ．
(1)、请直接写出A，B两点的坐标；(2)、如图2，点M是线段上的一个动点，点N是线段的一个定点，连接 ， ， 当点M在线段上移动时（不与A，C重合），探究 ， ， 之间的数量关系，并说明理由；(3)、在坐标轴上是否存在点P，使三角形的面积与三角形的面积相等？若存在，请求出点P的坐标；若不存在，试说明理由．20. 对于平面直角坐标系中的任意一点 ， 给出如下定义：记 ， 那么我们把点与点称为点的一对“和美点”．例如：点的一对“和美点”是点与点 ．
(1)、点的一对“和美点”坐标是与 ．(2)、若点的一对“和美点”重合，则的值为 ．(3)、若点的一个“和美点”坐标为 ， 求点的坐标．21. 如图，在直角坐标系中，已知点 ， 直线l是第二、四象限的角平分线．
(1)、操作：连结线段 ， 作出线段关于直线l的轴对称图形 ．(2)、发现：请写出坐标平面内任一点关于直线l的对称点的坐标．(3)、应用：请在直线l上找一点Q，使得最小，并写出点Q的坐标．22. 已知△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位长度，再向下平移6个单位长度得到△A1B1C1 ． (图中每个小方格边长均为1个单位长度) ．
(1)、在图中画出平移后的△A1B1C1；(2)、直接写出△A1B1C1各顶点的坐标．； ； ；
(3)、求出△ABC的面积23. 如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，得到A，B的对应点C，
D，连接AC，BD，CD.
(1)、直接写出点C，D的坐标为C（），D（）；(2)、四边形ABDC的面积为；(3)、动点P从点A出发，沿折线AO－OC－CD以每秒1个单位长的速度向终点D运动，运动时间为x(s).当三角形PAC的面积与三角形POB的面积相等时，求点P运动时间x的值.