浙教版数学八上第4章图形与坐标二阶单元测试卷

试卷更新日期：2024-11-03 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 如果小岛甲在小岛乙的东南方向20km处，那么小岛乙在小岛甲的( ).

A、西南方向20km处 B、西北方向20km处 C、东北方向20km处 D、正北方向20km处

查看试题解析
2. 已知点N(4，1-a)在第四象限，则a的取值范围是( ).

A、a>1 B、a≥1 C、a<1 D、a≤1

查看试题解析
3. 在平面直角坐标系中，若点A(a，-b)在第三象限，则点B(- ab，b)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 剪纸是中国古代最古老的民间艺术之一．如图是一张蕴含着轴对称变换的蝴蝶剪纸，点A与点B对称，点C与点D对称，将其放置在直角坐标系中，点A ， B ， C的坐标分别为 $(3, 0)$ ， $(5, 0)$ ， $(1, 4)$ ，则点D的坐标为（）

A、 $(7, 4)$ B、 $(6, 4)$ C、 $(5, 4)$ D、 $(4, 4)$

查看试题解析
5. 如果点 $P (2, b)$ 和点 $Q (a, - 3)$ 关于直线 $x = 1$ （平行于y轴的直线，直线上的每个点的横坐标都是1）对称，则 $a + b$ 的值是（）

A、 $- 3$ B、1 C、 $- 5$ D、5

查看试题解析
6. 如果点M（3a﹣9，1+a）是第二象限的点，则a的取值范围在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
7. 点P在第四象限，点P到x轴的距离是5，到y轴的距离是2，那么点P的坐标为（）

A、 $(5 ， - 2)$ B、 $(- 2 ， 5)$ C、 $(- 5 ， 2)$ D、 $(2 ， - 5)$

查看试题解析
8. 若点 $A (n - 1 ， n + 1)$ 在 $x$ 轴上，则点 $B (2 ， - n)$ 关于原点对称的点的坐标为（）

A、 $(- 2 ， 1)$ B、 $(- 2 ， - 1)$ C、 $(- 1 ， 2)$ D、 $(- 1 ， - 2)$

查看试题解析
9. 在平面直角坐标系中，将点 $A (x, y)$ 向左平移 $5$ 个单位长度，再向上平移 $3$ 个单位长度后与点 $B (- 3,2)$ 重合，则点 $A$ 的坐标是( )

A、 $(2,5)$ B、 $(- 8,5)$ C、 $(- 8, - 1)$ D、 $(2, - 1)$

查看试题解析
10. 如图，在平面直角坐标系中，一巡查机器人接到指令，从原点 $O$ 出发，沿着路线 $O \to A_{1} \to A_{2} \to A_{3} \to A_{4} \to A_{5} \to A_{6} \to A_{7} \to A_{8} \cdot \cdot \cdot \cdot \cdot \cdot$ 移动，每次移动 $1$ 个单位长度，依次得到 $A_{1} (0, 1) ， A_{2} (1, 1) ， A_{3} (1, 0) ， \cdot \cdot \cdot$ 根据这个规律，点 $A_{2024}$ 的坐标为（）

A、 $(1011, - 1)$ B、 $(1011, 0)$ C、 $(1012, - 1)$ D、 $(1012, 0)$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 已知点A的坐标为（﹣3，4），则A关于x轴的对称点A^'的坐标为．

查看试题解析
12. 点 $A (4 ， 2)$ 先向右平移4个单位，再向下平移1个单位后的坐标为

查看试题解析
13. 如图所示是一组密码的一部分.为了保密，许多情况下可采用不同的密码，请你运用所学知识找到破译的“钥匙”.目前，已破译出“今天考试”的真实意思是“努力发挥”，若“今”所对应的字为“努”，那么破译“正做数学”的真实意思是.

查看试题解析
14. 以二元一次方程组 ${\begin{cases} x + 3 y = 7 \\ y - x = 1 \end{cases}$ 的解为坐标点 $(x, y)$ ，在平面直角坐标系的第象限.

查看试题解析
15. 如图，在△ABC中，点A的坐标为（0，1），点B的坐标为（4，1），点C的坐标为（3，4），点D在第一象限（不与点C重合），且△ABD与△ABC全等，点D的坐标是．

查看试题解析
16. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（m，n），则经过第2021次变换后所得的A点坐标是．

查看试题解析

三、解答题（本题共8小题，第17题6分，第18题8分，第19题6分，第20题7分，第21题7分，第22题10分，第23题12分，第24题10分，共66分）

17. 如图，在阴影区域内(不包括边界)，写出横坐标和纵坐标都是整数的点的坐标，并指出各点所在的象限或坐标轴.

查看试题解析
18. 如图，方格纸中每个小方格都是边长为1个单位的正方形.已知△ABC的顶点均在格点上，建立直角坐标系，点A的坐标为(2，4).

(1)、直接写出点B，C，B₁ ， A₁的坐标.

(2)、△A₁B₁C是由△ABC经过怎样的变化得到的?写出变化过程.

(3)、作△BB₁C关于y轴对称的图形，点C的对称点为C₁ ，直接写出△AC₁A₁的形状.

查看试题解析
19. 在直角坐标系中，已知点P(a+1，3a-1).将点P先向下平移2个单位，再向左平移1个单位后得到点Q，若点Q在第一象限，求a的取值范围.

查看试题解析
20. 已知，点 $P (2 m - 6, m + 2)$ ．

(1)、若点P在y轴上，求点P的坐标；

(2)、若点P的纵坐标比横坐标大9，试判断点P在第几象限，并说明理由．

查看试题解析
21. 如图，四边形 $A B C D$ 各个顶点的坐标分别为 $(- 2, 8)$ ， $(- 11, 6)$ ， $(- 14, 0)$ ， $(0, 0)$ ．

(1)、求这个四边形的面积．

(2)、如果把原来四边形 $A B C D$ 各个顶点纵坐标保持不变，横坐标都增加2，所得的四边形面积又是多少？为什么？

查看试题解析
22. 如图，在 $6 \times 6$ 的正方形网格中，每个小正方形边长都是1，每个小正方形的顶点叫做格点．A，B，C三点均在格点上．请你以点A为坐标原点，水平向右为x轴正方向，竖直向上为y轴正方向，直接在图中建立平面直角坐标系．

(1)、点B的坐标为；

(2)、连接AB，将线段AB平移，使点B平移到点C的位置，点A平移到点D的位置，请在图中标出点D的位置，并写出点D的坐标；

(3)、求三角形ABD的面积．

查看试题解析
23. 在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示.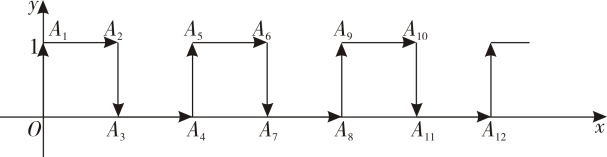

(1)、填写下列各点的坐标：A₁( ， )、A₃( ， )、A₁₂( ， )；

(2)、写出点A₄n的坐标(n是正整数)；

(3)、指出蚂蚁从点A₁₀₀到点A₁₀₁的移动方向.

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，对于点 $P$ ，给出如下定义：
点 $P$ 的“第 $I$ 类变换”：将点 $P$ 向左平移1个单位长度，再向上平移2个单位长度；
点 $P$ 的“第II类变换”：将点 $P$ 向右平移3个单位长度，再向下平移1个单位长度.

(1)、①已知点 $A (3, 0)$ ，对点 $A$ 进行1次“第 $I$ 类变换”后得到的点的坐标是；
②点 $B$ 为平面内一点，若对点 $B$ 进行1次“第II类变换”后得到点 $(0, 2)$ ，则点 $B$ 的坐标是.

(2)、已知点 $C (m, n)$ ，若对点 $C$ 连续进行5次“第 $I$ 类变换”，再连续进行4次“第II类变换”后得到点 $D$ ，求点 $D$ 的坐标(用 $m, n$ 表示).

(3)、点P的坐标 $(- 10, 3)$ ，对点 $P$ 进行“第 $I$ 类变换”和“第II类变换”共计20次后得到点 $Q$ ，请问是否存在一种上述两类变换的组合，使得点 $Q$ 恰好在 $y$ 轴上?如果存在，请求出此时点 $Q$ 的坐标；如果不存在，请说明理由.

查看试题解析

浙教版数学八上第4章 图形与坐标 二阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题6分，第18题8分，第19题6分，第20题7分，第21题7分，第22题10分，第23题12分，第24题10分，共66分）

浙教版数学八上第4章图形与坐标二阶单元测试卷