浙教版数学八上第4章 图形与坐标 一阶单元测试卷
试卷更新日期：2024-11-03 类型：单元试卷
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 下列表述中，能确定位置的是( ).A、小明的座位在教室里第3排 B、新华书店距学校800米 C、学校食堂在学校的北面 D、黑棋子在棋盘上位于第5列第3行2. 已知点P在直角坐标系的第二象限内，且点P到x轴的距离是3，到y轴的距离是2，则点P的坐标是( ).A、P(3，2) B、P(-3，2) C、P(-2，3) D、P(2，3)3. 如图，在第二象限内的点是( ).
A、P1 ， P2 ， P3 B、P1 ， P2 C、P1 ， P3 D、P14. 在直角坐标系中，将点(a，b)向上平移1个单位，再向左平移1个单位，所得的点的坐标是( ).A、(a+1，b-1) B、(a-1，b+1) C、(a-1，b-1) D、(a+1，b+1)5. 在平面直角坐标系中，将点向上平移2个单位长度后得到点的坐标为（ ）A、 B、 C、(3，3) D、(3，7)6. 若点在y轴上，则点在（ ）A、第四象限 B、第三象限 C、第二象限 D、第一象限7. 在平面直角坐标系中，将点向下平移个单位长度，再向右平移个单位长度，得到点 ， 则点的坐标是（ ）A、 B、 C、 D、8. 下表是计算机中一个Excel电子表格文件，计算B2 ， C2 ， D2 ， E2和F2的和，其结果是( ).A
B
C
D
E
F
1
4
6
2
5
9
3
2
2
3
4
5
6
7
A、28 B、25 C、15 D、109. 有一张方格纸，每个小方格的边长是厘米，上面堆叠有棱长厘米的小正方体如图 ， 小正方体的位置用表示，小正方体的位置用表示，那么小正方体的位置可以表示成( )
A、 B、 C、 D、无正确选项10. 在平面直角坐标系中，以方程组的解为坐标的点位于第三象限，则m的取值范围是（ ）A、 B、 C、 D、二、填空题（本题有6小题，每小题4分，共24分）
-
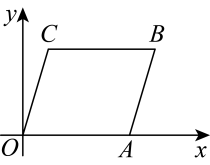
11. 将点关于轴对称后再向左平移个单位，其对应点落在轴上，则 ．12. 若点在y轴上，则 ．13. 已知点到两坐标轴的距离相等，则 ．14. 已知点和关于y轴对称，则的值为.15. 如图，已知点A，B的坐标分别为(2，0)，(0，1)，若将线段AB平移至A1B1 ， 则a+b的值为
16. 在直角坐标系中，我们将(-b，-a)称为(a，b)的“关联点”.例如，点(-2，-1)是点(1，2)的关联点.如果一个点和它的“关联点”在同一象限内，那么这一点在第象限.三、解答题（本题共8小题，第17题6分，第18题6分，第19题6分，第20题8分，第21题10分，第22题10分，第23题10分，第24题10分，共66分）
-
17. 已知在直角坐标系中，等边三角形ABC的两个顶点的坐标分别是A(1，0)，B(-1，0)，写出点C的坐标.18. 规定列号写在前面，行号写在后面，在图上标出位置是(2，1)，(5，2)和(4，5)的三个点(依次记为A，B，C)，并求出△ABC的面积.(图中每个小正方形的边长都是1)
19. 在直角坐标系中描出下列各点：A(-1，0)，B(0，2)，C(-2，3)，D(-3，-3)，E(2，-3)，F(4，0).在这些点中，哪些在x轴上，哪些在y轴上?并说明线段DE与y轴的关系.
20. 如图，在直角坐标系中，已知△ABC的顶点坐标为A(1，4)，B(-3，2)，C(-1，-1).△ABC中任意一点P(m，n)经过平移后的对应点为P1(m+4，n-3)，将△ABC作同样的平移得到△A1B1C1.
(1)、在图中画出△A1B1C1.(2)、写出点A1 ， B1 ， C1的坐标.21. 定义：在平面直角坐标系中，对于任意两点A(a ， b)， B(c ， d)，若点T(x ， y)满足 ， ， 那么称点T是点A和B的衍生点．例如：M (-2，5)，N(8，-2)，则点T (2，1)是点M和N的衍生点．已知点D (3，0)，点E (m ， m+2)，点T(x ， y)是点D和E的衍生点．
(1)、若点E (4，6)，则点T的坐标为 ；(2)、请直接写出点T的坐标(用m表示)；(3)、若直线ET交x轴于点H ， 当∠DHT=90°时，求点E的坐标．
