浙教版数学九年级上册期中模拟测试卷 C
试卷更新日期:2024-11-03 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过这个十字路口,则至少一辆车向右转的概率是( )A、 B、 C、 D、2. 抛物线y=ax2+bx+c的顶点为(﹣1,﹣2),抛物线与y轴的交点位于x轴上方.以下结论正确的是( )A、a<0 B、c<0 C、a﹣b+c=﹣2 D、b2﹣4ac=03. 如图, , 为的两条弦,连接 , , 若 , 则的度数为( )
 A、 B、 C、 D、4. 已知一元二次方程有两实根 , , 且 , 则下列结论中正确的有( )
A、 B、 C、 D、4. 已知一元二次方程有两实根 , , 且 , 则下列结论中正确的有( );
抛物线的顶点坐标为;
;
若 , 则 .
A、个 B、个 C、个 D、个5. 如图,正六边形ABCDEF内接于⊙O , OA=1,则AB的长为( ) A、2 B、 C、1 D、6. 抛物线y=(x﹣1)2+c经过(﹣2,y1),(0,y2),( , y3)三点,则y1 , y2 , y3的大小关系正确的是( )A、y1>y2>y3 B、y2>y3>y1 C、y3>y1>y2 D、y1>y3>y27. 如图,内接于⊙O , BC为⊙O的直径,AD平分交⊙O于D . 则的值为( )
A、2 B、 C、1 D、6. 抛物线y=(x﹣1)2+c经过(﹣2,y1),(0,y2),( , y3)三点,则y1 , y2 , y3的大小关系正确的是( )A、y1>y2>y3 B、y2>y3>y1 C、y3>y1>y2 D、y1>y3>y27. 如图,内接于⊙O , BC为⊙O的直径,AD平分交⊙O于D . 则的值为( ) A、 B、 C、 D、8. 如图,正方形的顶点A , C在抛物线上,点D在y轴上.若A , C两点的横坐标分别为m , n(),下列结论正确的是( )
A、 B、 C、 D、8. 如图,正方形的顶点A , C在抛物线上,点D在y轴上.若A , C两点的横坐标分别为m , n(),下列结论正确的是( ) A、 B、 C、 D、9. 如图,是的直径,是的弦,半径 , 连接 , 交于点E , , 则的度数是( )
A、 B、 C、 D、9. 如图,是的直径,是的弦,半径 , 连接 , 交于点E , , 则的度数是( ) A、 B、 C、 D、10. 如图,二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列四个结论:①;②;③;④当时,;其中正确结论的个数为( )
A、 B、 C、 D、10. 如图,二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列四个结论:①;②;③;④当时,;其中正确结论的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
11. 某校组织多项活动加强科学教育,八年级(一)班分两批次确定项目组成员,参加“实践探究”活动,第一批次确定了7人,第二批次确定了1名男生、2名女生.现从项目组中随机抽取1人承担联络任务,若抽中男生的概率为 , 则第一批次确定的人员中,男生为人.12. 如图,已知正六边形ABCDEF的边长为2,以点E为圆心,EF长为半径作圆,则该圆被正六边形截得的的长为 .
 13. 若二次函数的图象与轴有交点,则的取值范围是.14. 如图,是的弦,连接 , , 是所对的圆周角,则与的和的度数是 .
13. 若二次函数的图象与轴有交点,则的取值范围是.14. 如图,是的弦,连接 , , 是所对的圆周角,则与的和的度数是 . 15. 把二次函数y=2x2的图象向左平移1个单位长度,再向下平移2个单位长度,平移后抛物线的解析式为 .
15. 把二次函数y=2x2的图象向左平移1个单位长度,再向下平移2个单位长度,平移后抛物线的解析式为 .
16. 如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系的图象,点在图象上.若一辆箱式货车需在停车棚下避雨,货车截面看作长 , 高的矩形,则可判定货车完全停到车棚内(填“能”或“不能”).
三、解答题(共8题,共72分)
-
17. 某校举办“我劳动,我快乐,我光荣”活动.为了解该校九年级学生周末在家的劳动情况,随机调查了九年级1班的所有学生在家劳动时间(单位:小时),并进行了统计和整理绘制如图所示的不完整统计图.根据图表信息回答以下问题:
类别
劳动时间
A
B
C
D
E

 (1)、九年级1班的学生共有人,补全条形统计图;(2)、若九年级学生共有800人,请估计周末在家劳动时间在3小时及以上的学生人数;(3)、已知E类学生中恰好有2名女生3名男生,现从中抽取两名学生做劳动交流,请用列表或画树状图的方法,求所抽的两名学生恰好是一男一女的概率.18. 某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示.
(1)、九年级1班的学生共有人,补全条形统计图;(2)、若九年级学生共有800人,请估计周末在家劳动时间在3小时及以上的学生人数;(3)、已知E类学生中恰好有2名女生3名男生,现从中抽取两名学生做劳动交流,请用列表或画树状图的方法,求所抽的两名学生恰好是一男一女的概率.18. 某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示. (1)、求这段时间内y与x之间的函数解析式;(2)、在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大?最大利润是多少?19. 如图,是的外接圆,D是直径AB上一点,的平分线交AB于点E , 交于另一点F , .
(1)、求这段时间内y与x之间的函数解析式;(2)、在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大?最大利润是多少?19. 如图,是的外接圆,D是直径AB上一点,的平分线交AB于点E , 交于另一点F , . (1)、求证:;(2)、设 , 垂足为M , 若 , 求AC的长.20. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.
(1)、求证:;(2)、设 , 垂足为M , 若 , 求AC的长.20. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.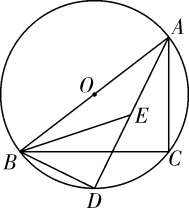 (1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.21. 如图1,抛物线()与轴交于 , 两点,与轴交于点 .
(1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.21. 如图1,抛物线()与轴交于 , 两点,与轴交于点 . (1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.22. 如图,已知是等边三角形的外接圆,连接并延长交于点 , 交于点 , 连接 , .
(1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.22. 如图,已知是等边三角形的外接圆,连接并延长交于点 , 交于点 , 连接 , . (1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.23. 根据背景素材,探索解决问题.
(1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.23. 根据背景素材,探索解决问题.平面直角坐标系中画一个边长为2的正六边形ABCDEF
背景素材
六等分圆原理,也称为圆周六等分问题,是一个古老而经典的几何问题,旨在解决如何使用直尺和圆规将一个圆分成六等份的问题.这个问题由欧几里得在其名著《几何原本》中详细阐述.
已知条件
点C与坐标原点O重合,点D在x轴的正半轴上且坐标为(2,0).
操作步骤
①分别以点C , D为圆心,CD长为半径作弧,两弧交于点P;
②以点P为圆心,PC长为半径作圆;
③以CD的长为半径,在⊙P上顺次截取;
④顺次连接DE , EF , FA , AB , BC . 得到正六边形ABCDEF .

问题解决
任务一
根据以上信息,请你用不带刻度的直尺和圆规,在图中完成这道作图题(保留作图痕迹,不写作法)
任务二
将正六边形ABCDEF绕点D顺时针旋转60°,直接写出此时点E所在位置的坐标: .
24. 如图,抛物线经过点和点 , 与轴的另一个交点为 , 连接、 .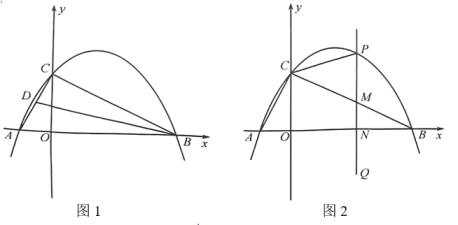 (1)、求抛物线的解析式及点的坐标;(2)、如图1,若点是线段的中点,连接 , 在轴上是否存在点 , 使得是以为斜边的直角三角形?若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,点是第一象限内抛物线上的动点,过点作轴,分别交、轴于点、 , 当中有某个角的度数等于度数的2倍时,请求出满足条件的点的横坐标.
(1)、求抛物线的解析式及点的坐标;(2)、如图1,若点是线段的中点,连接 , 在轴上是否存在点 , 使得是以为斜边的直角三角形?若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,点是第一象限内抛物线上的动点,过点作轴,分别交、轴于点、 , 当中有某个角的度数等于度数的2倍时,请求出满足条件的点的横坐标.