浙教版数学八上第3章一元一次不等式一阶单元测试卷

试卷更新日期：2024-11-03 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 若a>b，则下列式子正确的是( ).

A、-5a>-5b B、a-3>b-3 C、4-a>4-b D、 $\frac{1}{2} a < \frac{1}{2} b$

查看试题解析
2. 由a>b能得到am>bm成立的条件是( ).

A、m>0 B、m<0 C、m≥0 D、m≠0

查看试题解析
3. 关于x的不等式的解在数轴上的表示如图所示，则该不等式的解是( ).

A、-2<x<1 B、-2<x≤1 C、-2≤x<1 D、-2≤x≤1

查看试题解析
4. 不等式x>2在数轴上表示正确的是( ).

A、 B、 C、 D、

查看试题解析
5. 设某数为x，它的一半与它 $\frac{2}{3}$ 的差大于-1的相反数，可列出不等式为( ).

A、 $\frac{1}{2} x - \frac{2}{3} x > 1$ B、 $\frac{1}{2} x - \frac{2}{3} x > - 1$ C、 $\frac{2}{3} x - \frac{1}{2} x > 1$ D、 $\frac{1}{2} (x - \frac{2}{3} x) > - 1$

查看试题解析
6. 如图，数轴上所表示的不等式组的解集是（）

A、 $x > - 1$ B、 $- 1 < x \leq 2$ C、 $- 1 \leq x \leq 2$ D、 $x \leq 2$

查看试题解析
7. 四个小朋友玩跷跷板，他们的体重分别为P，Q，R，S，如图所示，则他们的体重大小关系是

A、P>R>S>Q B、Q>S>P>R C、S>P>Q>R D、S>P>R>Q

查看试题解析
8. 某市区现行出租车的收费标准：起步价5元(即行驶距离不超过3千米都需付5元车费)，超过3千米后，每增加1千米，加收1.2元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费11元，那么甲地到乙地路程的最大值是( ).

A、5千米 B、7千米 C、8千米 D、9千米

查看试题解析
9. 若关于x的分式方程 $\frac{2 x - a}{x - 2} = \frac{1}{2}$ 的解为非负数，则a的取值范围是( ).

A、a≥1 B、a>1 C、a≥1且a≠4 D、a>1且a≠4

查看试题解析
10. 如果关于 $y$ 的方程 $\frac{a - (1 - y)}{3} = y - 2$ 有非负整数解，且关于 $x$ 的不等式组 $\{\begin{array}{l} \frac{x - a}{2} ⩾ 2 \\ x - 4 ⩽ 3 (x - 2) \end{array}$ 的解集为 $x ⩾ 1$ ，则所有符合条件的整数 $a$ 的和为( )

A、 $- 5$ B、 $- 8$ C、 $- 9$ D、 $- 12$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 不等式 $\frac{4 x - 5}{11} < 1$ 的正整数解为.

查看试题解析
12. 若关于x的分式方程 $\frac{2 x - m}{x + 1} = 3$ 的解是负数，则字母m的取值范围是.

查看试题解析
13. 有一个两位数，个位数字与十位数字的和是9.且这个两位数不小于81，这个两位数是.

查看试题解析
14. 某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设不计其他费用，如果超市至少获得20%的利润，那么这种水果的售价在进价的基础上应至少提高%.

查看试题解析
15. 不等式组 $\{\begin{matrix} x > a, \\ x \geq b \end{matrix}$ 的解在数轴上表示如图所示，则不等式组 $\{\begin{matrix} x < a, \\ x \leq b \end{matrix}$ 的解是.

查看试题解析
16. 按下面的程序进行运算.
规定：程序运行到“判断结果是否大于35”为一次运算.若运算进行了5次才停止，x是整数，则x的值是.

查看试题解析

三、解答题（本题共8小题，第17题6分，第18题7分，第19题6分，第20题6分，第21题10分，第22题10分，第23题9分，第24题12分，共66分）

17. 已知a>b，试比较-2a+3与-2b+3的大小，并说明理由.

查看试题解析
18. 为了庆祝国庆，学校准备举办“我和我的祖国”演讲比赛．学校计划为比赛购买A、B两种奖品．已知购买1个A种奖品和4个B种奖品共需120元；购买5个A种奖品和6个B种奖品共需250元．

(1)、求A，B两种奖品的单价．

(2)、学校准备购买A，B两种奖品共60个，且B种奖品的数量多于A种奖品数量的 $\frac{1}{3}$ ，购买预算不超过1285元，请问学校有哪几种购买方案．

查看试题解析
19. 解下列不等式（组）：

(1)、 $3 x - 1 > \frac{x + 1}{3}$

(2)、 $\{\begin{matrix} 2 (x - 6) < 3 - x ① \\ \frac{x - 1}{2} \leq 2 (x + 1) - 7 ② \end{matrix}$

查看试题解析
20. 小军将不等式a<0进行如下的变形：
两边都加上a，得a+a<a，即2a<a.①
两边都除以a，得2<1.②
2怎么会小于1呢?小军糊涂了……聪明的同学，小军的解题过程错在哪一步?请予以改正.

查看试题解析
21. 某工厂准备用图甲所示的A型正方形板材和B型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子．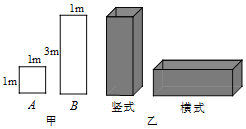

(1)、若该工厂准备用不超过10000元的资金去购买A，B两种型号板材，并全部制作竖式箱子，已知A型板材每张30元，B型板材每张90元，求最多可以制作竖式箱子多少只？

(2)、若该工厂仓库里现有A型板材65张、B型板材110张，用这批板材制作两种类型的箱子，问制作竖式和横式两种箱子各多少只，恰好将库存的板材用完？

(3)、若该工厂新购得65张规格为 $3 \times 3 m$ 的C型正方形板材，将其全部切割成A型或B型板材 $($ 不计损耗 $)$ ，用切割成的板材制作两种类型的箱子，要求竖式箱子不少于20只，且材料恰好用完，则能制作两种箱子共只 $.$

查看试题解析
22. 解不等式： ${\begin{array}{l} 2 (x + 1) > x ① \\ 1 - 2 x \geq \frac{x + 7}{2} ② \end{array}$ ．请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为．

查看试题解析
23. 李大爷在龙岭街有若干间房屋出租，每间房的租金相同，2022年共收租金 $10.2$ 万元，2023年因房屋租售行情不好，每间房租金比2022年降低了1000元，2023 年共收租金 $9.6$ 万元．

(1)、李大爷一共有几间房屋出租?

(2)、2024年李大爷再次降低房屋租金，但希望年租金不少于 $8.4$ 万元，则每间房再次降低房屋租金最多可降多少元?

查看试题解析

24. 根据以下素材，探索完成任务1和任务2：

主题：奶茶销售方案制定问题
年轻人喜欢喝奶茶，入夏之际某知名奶茶品牌店推出两款爆款水果茶“满杯杨梅”和“芝士杨梅”．
素材1	两款奶茶配料表如下：
	芝士杨梅	配料
	19元/杯	芝士 $100 ml$ /杯
		茉莉清茶 $400 m l$ /杯
		杨梅肉
		多肉

	满杯杨梅	配料
	17元/杯	茉莉清茶 $500 ml$ /杯
		杨梅肉
		多肉
素材2	9月2日当天销售“芝士杨梅”共获利润400元，“满杯杨梅”共获利润480元，其中每杯“芝士杨梅”的利润是每杯“满杯杨梅”的 $\frac{5}{4}$ 倍，“满杯杨梅”比“芝士杨梅”多卖20杯．
素材3	由于芝士保质期将至，为了去库存，9月3日决定对“芝士杨梅”每杯降价4元促销，并要求当天芝士消耗量不少于 $3500 m l$ ，配制的 $17500 m l$ 茉莉清茶全部用于制作“芝士杨梅”和“满杯杨梅”．
问题解决
任务1	确定奶茶的利润	每杯“芝士杨梅”和“满杯杨梅”的利润是多少？
任务2	拟定最优方案	为了使9月3日这两种奶茶获利最大，需制做“芝士杨梅”和“满杯杨梅”共多少杯？

查看试题解析

浙教版数学八上第3章 一元一次不等式 一阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题6分，第18题7分，第19题6分，第20题6分，第21题10分，第22题10分，第23题9分，第24题12分，共66分）

浙教版数学八上第3章一元一次不等式一阶单元测试卷