浙教版数学九上第4章相似三角形三阶单元测试卷

试卷更新日期：2024-11-03 类型：单元试卷

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 1765年数学家欧拉在其著作《三角形几何学》中首次提出定理：三角形三边的垂直平分线的交点，三条中线的交点以及三条高线的交点在一条直线上，这条线也被称为欧拉线.如图，已知 $△ O A B$ 的三个顶点分别为 $O (0, 0)$ ， $A (2, 4)$ ， $B (6, 0)$ ，则 $△ O A B$ 的欧拉线的解析式为（）

A、 $y = 2 x - 2$ B、 $y = \frac{x}{3}$ C、 $y = - x + 4$ D、 $y = - 2 x + \frac{20}{3}$

查看试题解析
2. 如图， $△ A B C$ 中， $A B = B C = 1$ ， $∠ C = 72 °$ .将 $△ A B C$ 绕点A顺时针旋转得到 $△ A B^{'} C^{'}$ ，点 $B'$ 与点B是对应点，点 $C^{'}$ 与点C是对应点.若点 $C^{'}$ 恰好落在BC边上，下列结论：①点B在旋转过程中经过的路径长是 $\frac{1}{5} π$ ；② $B^{'} A / / B C$ ；③ $B D = C^{'} D$ ；④ $\frac{A B}{A C} = \frac{B^{'} B}{B D}$ .其中正确的结论是( )

A、①②③④ B、①②③ C、①③④ D、②④

查看试题解析
3. 如图，边长为 5 的正方形 $A B C D, E, F, G, H$ 分别为各边中点. 连接 $A G, B H, C E, D F$ ，交点分别为 $M, N, P, Q$ ，那么四边形 $M N P Q$ 的面积为（）

A、1 B、2 C、5 D、10

查看试题解析
4. 如图， $△ A B C$ 中 $∠ B A C = 60 °$ ，分别以 $A B ， A C$ 为边向外侧作等边三角形 $A B E$ 和等边三角形 $A C D ， M 、 N$ 分别是 $B E ， C D$ 的中点，连结 $M N ， B D$ ，若要知道 $M N$ 的值，只需知道下列哪个值（）

A、 $△ A B C$ 的面积 B、 $△ A B D$ 的面积 C、线段 $B C$ 的长 D、线段 $B D$ 的长

查看试题解析
5. 如图，正方形ABCD的边长是3，BP＝CQ ，连接AQ ， DP交于点O ，并分别与边CD ， BC交于点F ， E ，连接AE ，下列结论正确的是（　　）

A、OA²＝OE•OP B、OQ²＝OA•OF C、若BP＝1，则OE＝2 D、若BP＝1，则 $O Q = \frac{13}{5}$

查看试题解析
6. 若一个三角形一条边的平方等于另两条边的乘积，我们把这个三角形叫做比例三角形．有下列结论：
①已知 $△ A B C$ 是比例三角形， $A B = 4$ ， $B C = 5$ ，那么 $A C = 2 \sqrt{5}$ ；
②在 $△ A B C$ 中，点 $D$ 在 $A C$ 上，且 $A D = B C$ ， $∠ A B D = ∠ C$ ，那么 $△ A B C$ 是比例三角形；
③如图，在四边形 $A B C D$ 中，已知 $A D ∥ B C$ ， BD平分 $∠ A B C$ ， $A B ⊥ A C$ ， $A D ⊥ C D$ ，那么 $△ A B C$ 是比例三角形；
④已知直线 $y = \sqrt{3} x + 3 \sqrt{3}$ 与 $x$ 轴、 $y$ 轴交于点 $A 、 B$ ，点 $C (3, 0)$ ，那么 $△ A B C$ 是比例三角形．
其中，正确的个数是（）

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
7. 【情境】如图是某数学项目学习小组设计的“鱼跃龙门”徽章图案，已知A，B，C，D，E是圆的5个等分点，连结BD，CE交于点 $F$ .设鱼头部分的四边形ABFE的面积为 $S_{1}$ ，鱼尾部分的 $△ C D F$ 的面积为 $S_{2}$ .
【问知】设 $S_{1} : S_{2} = n : 1$ ，则 $n$ 的值为（）

A、 $4 \sqrt{3} - 1$ B、 $3 + \sqrt{5}$ C、 $1 + 2 \sqrt{5}$ D、 $3 \sqrt{5} - 1$

查看试题解析
8. 如图，四边形 $A B C D$ 与四边形 $C E F G$ 都是正方形， $A D$ 与 $E C$ 交于M点，延长 $C D$ 交 $E F$ 于N点，再连结 $N G 、 A E 、 D G$ ，若A、B、E共线，A、D、G共线，M为 $C E$ 中点， $S_{△ A M E} = 2$ ，则 $△ D N G$ 的面积为（）

A、10 B、11 C、12 D、13

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $B C = 3$ ，点E是边 $A C$ 上一动点，过点E作 $E F / / A B$ 交 $B C$ 于点F ， D为线段 $E F$ 的中点，按下列步骤作图：①以A为圆心，适当长为半径画弧交 $A B$ ， $A C$ 于点M ， N；②分别以M ， N为圆心，大于 $\frac{1}{2} M N$ 为半径画弧，两弧的交点为G；③作射线 $A G$ ．若射线 $A G$ 经过点D ，则 $A E$ 的长度为（）

A、 $\frac{8}{13}$ B、 $\frac{15}{13}$ C、 $\frac{20}{13}$ D、 $\frac{25}{13}$

查看试题解析
10. 如图，点A ， B分别在反比例函数 $y = \frac{2}{x} (x > 0)$ ， $y = - \frac{8}{x} (x > 0)$ 的图象上，且 $O A ⊥ O B$ ，则 $s i n B$ 的值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{10}}{10}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 如图，在△ABC中，AC＝2，AB＝3，直线CM∥AB ， E是BC上的动点（端点除外），射线AE交CM于点D ．在射线AE上取一点P ，使得AP＝2ED ，作PQ∥AB ，交射线AC于点Q ．设AQ＝x ， PQ＝y ．当x＝y时，CD＝；在点E运动的过程中，y关于x的函数表达式为．

查看试题解析
12. 如图，在边长为6的正方形ABCD中， $E$ 是CD边上一点，连接BE，在BE上取一点 $F$ ，使 $∠ B A F = 2 ∠ C B E$ ，过点 $F$ 作 $F G ⊥ B E$ 交CD于点 $G$ ，若 $E G = 2$ ， $∠ B A F \neq 6 0^{°}$ 时，则 $D E =$ .

查看试题解析
13. 如图，已知点 $A (- 7,0), B (x, 10), C (- 17, y)$ ，在平行四边形 $A B C O$ 中，它的对角线 $O B$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象相交于点 $D$ ，且 $O D : O B = 1 : 4$ ，则 $k =$ .

查看试题解析
14. △DEF为等边三角形，分别延长FD ， DE ， EF ，到点A ， B ， C ，使DA＝EB＝FC ，连接AB ， AC ， BC ，连接BF并延长交AC于点G ．若AD＝DF＝2，则∠DBF＝， FG＝．

查看试题解析
15. 如图，正方形 $A B C D$ 中， $A B = 3$ ，点 $E$ 在 $B C$ 的延长线上，且 $C E = 2$ ．连接 $A E$ ， $∠ D C E$ 的平分线与 $A E$ 相交于点 $F$ ，连接 $D F$ ，则 $D F$ 的长为．

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $△ A B C$ 的一条角平分线， $E$ 为 $A D$ 中点，连接 $B E$ .若 $B E = B C$ ， $C D = 2$ ，则 $B D =$ .

查看试题解析

三、解答题（本题共8小题，第17题9分，第18题9分，第19题9分，第20题9分，第21题6分，第22题9分，第23题6分，第24题9分，共66分）

17. 如图1，点 $P$ 是正方形 $A B C D$ 内一点， $C P = C B$ ，

(1)、填表∶
$∠ P C B$ 的度数
$30 °$
$x °$
$∠ B P D$ 的度数

(2)、若 $∠ A P D = 90 °$ ，求 $\frac{P A}{P D}$ 的值；

(3)、如图2，作 $C M ⊥ P D$ 于 $H$ ，交 $B P$ 延长线于点 $M$ ，已知 $B C = 5$ ， $B P = \sqrt{2}$ ，求 $A M$ 的长．

查看试题解析
18. 如图是由小正方形组成的8×8网格，每个小正方形的顶点叫做格点，图中B，C都是格点．仅用无刻度的直尺在给定网格中完成画图．

(1)、请在BC上方找到点A，使△ABC是一个以BC为斜边的等腰直角三角形

(2)、请在线段BC上找一点D使BD=2CD

(3)、已知E，F分别为AB，AC上两动点，且AE=AF，为探究E点在何处时DE+DF最小，请你完成如下步骤：①将点D绕A点逆时针旋转90°得D^' ，并连接DD^'交AC于F；②再在AB上找到点E使AE=AF即可确定E点位置

查看试题解析
19. 定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．

(1)、如图1，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $△ A B C$ 的角平分线，E，F分别是 $B D$ ， $A D$ 上的点．求证：四边形 $A B E F$ 是邻余四边形．

(2)、如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形 $A B E F$ ，使 $A B$ 是邻余线，E，F在格点上．

(3)、如图3，在（1）的条件下，取 $E F$ 中点M，连接 $D M$ 并延长交 $A B$ 于点Q，延长 $E F$ 交 $A C$ 于点N．若N为 $A C$ 的中点， $C D = 3 B E ， Q B = 6$ ，求邻余线 $A B$ 的长．

查看试题解析
20. 如图，已知 $A (- 2, - 2)$ ， $B (n, 4)$ 是一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 图象的两个交点，直线 $A B$ 与 $y$ 轴交于点 $C$ ．

(1)、求反比例函数和一次函数的表达式；

(2)、 $M$ 是 $y$ 轴上一点，且 $S_{△ M O B} = S_{△ A O B}$ ，求点 $M$ 的坐标；

(3)、在坐标轴上是否存在一点 $N$ ，使 $△ A B N$ 是以 $A B$ 为直角边的直角三角形？直接写出点 $N$ 的坐标．

查看试题解析
21. 问题情景：如图直角 $△ A C D$ 中， $∠ C = 90 °$ ， $A C = 1$ ， $∠ A = 22.5 °$ ，求 $C D$ 的长？
解题思路：把 $22.5 °$ 的角转化成特殊角度，再利用特殊角度进行边之间的换算．
解决方案：方法一：延长 $C D$ 至 $B$ ，使得 $∠ C A D = ∠ B A D$ ，过 $D$ 作 $D E ⊥ A B$ ，交 $A B$ 于点 $E$ ，根据角平分线的性质定理和等腰直角三角形边的关系，可得 $C D = D E = E B = \sqrt{2} - 1$
方法二：作 $A D$ 的中垂线交 $A C$ 于点 $F$ ，连接 $D F$ ，根据中垂线的性质定理和等腰直角三角形边的关务，设 $D C = x$ ， $C F = C D = x$ ， $A F = D F = 1 - x$ ， $D F = \sqrt{2} C F$ ，得 $1 - x = \sqrt{2} x$ ， $x = \sqrt{2} - 1$ ，则 $C D = \sqrt{2} - 1$ ．
其他方法……
迁移应用解决新问题：如图直角 $△ A C D$ 中， $∠ C = 90 °$ ， $A C = 1$ ， $∠ A = 15 °$ ，求 $C D$ 的长，写出你的解答过程．

查看试题解析
22. 【问题呈现】
$△ C A B$ 和 $△ C D E$ 都是直角三角形， $∠ A C B = ∠ D C E = 90 ° ， C B = m C A ， C E = m C D$ ，连接 $A D$ ， $B E$ ，探究 $A D$ ， $B E$ 的位置关系．

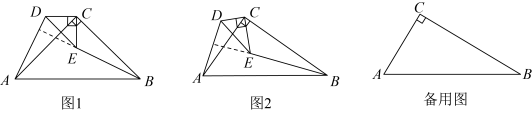(1)、如图1，当 $m = 1$ 时，直接写出 $A D$ ， $B E$ 的位置关系：；

(2)、如图2，当 $m \neq 1$ 时，（1）中的结论是否成立？若成立，给出证明；若不成立，说明理由．

(3)、【拓展应用】
当 $m = \sqrt{3} ， A B = 4 \sqrt{7} ， D E = 4$ 时，将 $△ C D E$ 绕点C旋转，使 $A ， D ， E$ 三点恰好在同一直线上，求 $B E$ 的长．

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中， $P$ 是 $A B$ 上一点（不与点 $A ， B$ 重合）， $C P = C D$ ，过点 $P$ 作 $P Q ⊥ C P$ ，交 $A D$ 于点 $Q$ ，连接 $C Q ， ∠ B P C = ∠ A Q P$ .

(1)、求证：四边形 $A B C D$ 是矩形.

(2)、当 $A P = 3 ， A D = 9$ 时，求 $A Q$ 和 $C Q$ 的长.

查看试题解析
24. 如图，点 $A 、 B 、 M 、 E 、 F$ 依次在直线 $l$ 上，点 $A 、 B$ 固定不动，且 $A B = 2$ ，分别以 $A B 、 E F$ 为边在直线 $l$ 同侧作正方形 $A B C D$ 、正方形 $E F G H$ ， $∠ P M N = 90^{\circ}$ ，直角边 $M P$ 恒过点 $C$ ，直角边 $M N$ 恒过点 $H$ ．

(1)、如图 $1$ ，若 $B E = 10$ ， $E F = 12$ ，求点 $M$ 与点 $B$ 之间的距离；

(2)、如图 $1$ ，若 $B E = 10$ ，当点 $M$ 在点 $B 、 E$ 之间运动时，求 $H E$ 的最大值；

(3)、如图 $2$ ，若 $B F = 22$ ，当点 $E$ 在点 $B 、 F$ 之间运动时，点 $M$ 随之运动，连接 $C H$ ，点 $O$ 是 $C H$ 的中点，连接 $H B 、 M O$ ，则 $2 O M + H B$ 的最小值为．

查看试题解析

$∠ P C B$ 的度数	$30 °$	$x °$
$∠ B P D$ 的度数

浙教版数学九上第4章 相似三角形 三阶单元测试卷

一、选择题（本题有10小题，每小题3分，共30分）

二、填空题（本题有6小题，每小题4分，共24分）

三、解答题（本题共8小题，第17题9分，第18题9分，第19题9分，第20题9分，第21题6分，第22题9分，第23题6分，第24题9分，共66分）

浙教版数学九上第4章相似三角形三阶单元测试卷