浙教版数学九年级上册期中模拟测试卷 B
试卷更新日期:2024-11-03 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 二次函数 的图象的对称轴是( )A、 B、 C、 D、2. 同一平面内,已知的直径是 , 线段 , 则点与的位置关系是( )A、点在外 B、点在上 C、点在内 D、不能确定3. 已知二次函数的图象如图所示,有下列4个结论:①;②;③;④关于x的方程有四个根,且这四个根的和为4,其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个4. 如图,已知是的弦, , 连接并延长交于点 , 则的度数是( )
A、1个 B、2个 C、3个 D、4个4. 如图,已知是的弦, , 连接并延长交于点 , 则的度数是( ) A、60° B、80° C、100° D、120°5. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( )
A、60° B、80° C、100° D、120°5. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( ) A、6 B、3 C、2 D、1.5
A、6 B、3 C、2 D、1.5二、填空题(每题3分,共18分)
-
6. 二次函数 的顶点坐标是 .7. 一个不透明的袋子中装有若干个红球和6个黄球,它们除颜色外都相同,从中随机摸出一个球,记下颜色后放回,通过大量反复实验发现,摸到黄球的频率约为0.3,由此推测这个袋中红球的个数为.8. 如图,已知二次函数y=ax2+bx+c(a<0)的图象与x轴交于不同两点,与y轴的交点在y轴正半轴,它的对称轴为直线x=1.有以下结论:①abc>0,②a+c>0,③若点(﹣1,y1)和(2,y2)在该图象上,则y1<y2 , ④设x1 , x2是方程ax2+bx+c=0的两根,若am2+bm+c=p,则p(m﹣x1)(m﹣x2)≤0.其中正确的结论是(填入正确结论的序号)。
 9. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、BC、BD . 若∠BCD=20°,则∠ABD=°.
9. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、BC、BD . 若∠BCD=20°,则∠ABD=°. 10. 如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为cm.
10. 如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为cm.
三、解答题(共7题,共72分)
-
11. 请阅读下列材料,并完成相应的任务.
克罗狄斯·托勒密(约90年- 168 年),古希腊天文学家、地理学家和光学家,在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:
圆的内接四边形的两条对角线的乘积等于两组对边乘积的和,即:如图1,若四边形ABCD
内接于⊙O,则有
任务:
(1)、材料中划横线部分应填写的内容为(2)、已知,如图2,四边形ABCD内接于⊙O,BD平分∠ABC,∠COD=120%,求证:BD=AB+BC 12. 在平面直角坐标系xOy中,点P(2,﹣3)在二次函数y=ax2+bx﹣3(a>0)的图象上,记该二次函数图象的对称轴为直线x=m .(1)、求m的值;(2)、若点Q(m , ﹣4)在y=ax2+bx﹣3的图象上,将该二次函数的图象向上平移5个单位长度,得到新的二次函数的图象.当0≤x≤4时,求新的二次函数的最大值与最小值的和;(3)、设y=ax2+bx﹣3的图象与x轴交点为(x1 , 0),(x2 , 0)(x1<x2).若4<x2﹣x1<6,求a的取值范围.13. 如图所示,四边形是半径为R的的内接四边形,是的直径, , 直线l与三条线段、、的延长线分别交于点E、F、G.且满足 .
12. 在平面直角坐标系xOy中,点P(2,﹣3)在二次函数y=ax2+bx﹣3(a>0)的图象上,记该二次函数图象的对称轴为直线x=m .(1)、求m的值;(2)、若点Q(m , ﹣4)在y=ax2+bx﹣3的图象上,将该二次函数的图象向上平移5个单位长度,得到新的二次函数的图象.当0≤x≤4时,求新的二次函数的最大值与最小值的和;(3)、设y=ax2+bx﹣3的图象与x轴交点为(x1 , 0),(x2 , 0)(x1<x2).若4<x2﹣x1<6,求a的取值范围.13. 如图所示,四边形是半径为R的的内接四边形,是的直径, , 直线l与三条线段、、的延长线分别交于点E、F、G.且满足 .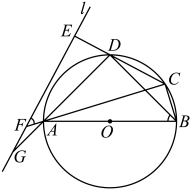 (1)、求证:直线直线;(2)、若;
(1)、求证:直线直线;(2)、若;①求证:;
②若 , 求四边形的周长.
14. 阅读下列材料:已知:如图1,等边△A1A2A3内接于⊙O,点P是弧A1A2上的任意一点,连接PA1 , PA2 , PA3 , 可证:PA1+PA2=PA3 , 从而得到: 是定值.
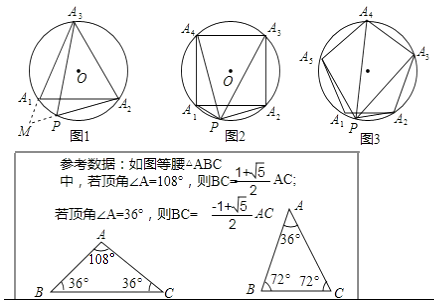 (1)、以下是小红的一种证明方法,请在方框内将证明过程补充完整;
(1)、以下是小红的一种证明方法,请在方框内将证明过程补充完整;证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1 , ∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M

∴PA3=MA2=PA2+PM=PA2+PA1 .
∴ ,是定值.
(2)、延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4”,其余条件不变,请问: 还是定值吗?为什么?(3)、拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则 =(只写出结果).15. 在初中函数学习中,我们经历了列表、描点、连线画函数图象,结合图象研究函数性质并对其性质进行应用的过程.小丽同学学习二次函数后,对函数y=x2-2|x|(自变量x可以是任意实数)图象与性质进行了探究.请同学们阅读探究过程并解答:(1)、作图探究:①下表是y与x的几组对应值:
x
……
-4
-3
-2
-1
0
1
2
3
4
……
y
……
8
3
0
m
0
-1
0
n
8
……
m= ▲ , n= ▲
②在平面直角坐标系×Oy中,描出表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象:
 (2)、深入思考:
(2)、深入思考:根据所作图象,回答下列问题:
①方程x2-2|x|= 0的解是;
②如果y=x2-2|x|的图象与直线y=k有4个交点,则k的取值范围是;
(3)、延伸思考:将函数y=x2-2|x|的图象经过怎样的平移可得到y1= (x+1)2- 2|x+1|-2的图象?请写出平移过程.