浙教版数学九年级上册期中模拟测试卷 A

试卷更新日期：2024-11-02 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列事件时必然事件的是( )

A、打开电视机，中央台正在播放“嫦娥六号完成人类首次背月采样”的新闻 B、从两个班级中任选三名学生担任学校安全督查员，至少有两名学生来自同一个班级 C、小明在内江平台一定能抢到龙舟节开幕式门票 D、从《西游记》《红楼梦》《三国演义》《水浒传》这四本书中随机抽取一本是《三国演义》

查看试题解析
2. 将抛物线y＝x²+2x﹣1向右平移3个单位后得到新抛物线的顶点坐标为（）

A、（﹣4，﹣1） B、（﹣4，2） C、（2，1） D、（2，﹣2）

查看试题解析
3. 如图，AB是⊙O的直径，∠E＝35°，则∠BOD＝（）

A、80° B、100° C、120° D、110°

查看试题解析
4. 某校八年级3班承担下周学校升旗任务，老师从备选的甲、乙、丙、丁四名同学中，选择两名担任升旗手，则甲、乙两名同学同时被选中的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
5. 在同一平面直角坐标系中，函数y＝ax﹣b（a≠0）和y $= \frac{- c}{x}$ （c≠0）的图象大致如图所示，则函数y＝ax²+bx+c（a≠0）的图象大致为（）

A、 B、 C、 D、

查看试题解析
6. 如图，AB是⊙O的直径，若 $∠ C D B = 60 °$ ，则 $∠ A B C$ 的度数等于（）

A、30° B、45° C、60° D、90°

查看试题解析
7. 如图，分别延长圆内接四边形ABCD的两组对边，延长线相交于点E ， F ．若∠E＝54°41'，∠F＝43°19'，则∠A的度数为（）

A、42° B、41°20' C、41° D、40°20'

查看试题解析
8. 两个半径相等的半圆按如图方式放置，半圆 $O^{^{'}}$ 的一个直径端点与半圆 $O$ 的圆心重合.若半圆的半径为2，则阴影部分的面积是（）

A、 $\frac{4}{3} π - \sqrt{3}$ B、 $\frac{4}{3} π$ C、 $\frac{2}{3} π - \sqrt{3}$ D、 $\frac{4}{3} π - \frac{\sqrt{3}}{4}$

查看试题解析
9. 如图，在等腰三角形ABC中， $A B = A C = 10, ∠ C = 7 0^{°}$ ，以AB为直径作半圆，与AC，BC分别相交于点D，E，则 $\overset{⌢}{D E}$ 的长度为（）

A、 $\frac{π}{9}$ B、 $\frac{5 π}{9}$ C、 $\frac{10 π}{9}$ D、 $\frac{25 π}{9}$

查看试题解析
10. 如图， $C D$ 是 $⊙ O$ 的直径，点 $A$ 、 $B$ 在 $⊙ O$ 上．若 $\overset{⌢}{A C} = \overset{⌢}{B C}$ ， $∠ A O C = 3 6^{∘}$ ，则 $∠ D =$ （）

A、 $9^{∘}$ B、 $1 8^{∘}$ C、 $3 6^{∘}$ D、 $4 5^{∘}$

查看试题解析

二、填空题（每题3分，共18分）

11. 为考察一种枸杞幼苗的成活率，在同一条件下进行移植试验，结果如下表所示：
移植总数 $n$
40
150
300
500
700
1000
1500
成活数 $m$
35
134
271
451
631
899
1350
成活的频率 $\frac{m}{n}$
0.875
0.893
0.903
0.902
0.901
0.899
0.900
估计这种幼苗移植成活的概率是(结果精确到0.1).

查看试题解析
12. 如图，四边形ABCD为平行四边形，以点A为圆心，AB长为半径画弧，交BC边于点E ，连接AE ， AB＝1，∠D＝60°，则 $\hat{B E}$ 的长l＝（结果保留π）．

查看试题解析
13. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+3与x轴相交于点A ， B ，点B的坐标为（3，0），若点C（2，3）在抛物线上，则AB的长为．

查看试题解析
14. 如图，四边形ABCD内接于⊙O，若四边形AOCD是菱形，∠B的度数是．

查看试题解析
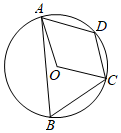15. 如图，抛物线 $y = a x^{2} + b x + c$ 的顶点A的坐标为 $(- \frac{1}{3}, n)$ ，与x轴的一个交点位于0和1之间，则以下结论：① $a b c > 0$ ；② $5 b + 2 c < 0$ ；③若抛物线经过点 $(- 6, y_{1})$ ， $(5, y_{2})$ ，则 $y_{1} > y_{2}$ ；④若关于x的一元二次方程 $a x^{2} + b x + c = 4$ 无实数根，则 $n < 4$ .其中正确结论是（请填写序号）.

查看试题解析
16. 抛物线 $y = a x^{2} + b x + c$ （a ， b ， c是常数， $a < 0$ ）经过 $(- 1, 1)$ ， $(m, 1)$ 两点，且 $0 < m < 1$ ．下列四个结论：
① $b > 0$ ；
②若 $0 < x < 1$ ，则 $a (x - 1)^{2} + b (x - 1) + c > 1$ ；
③若 $a = - 1$ ，则关于x的一元二次方程 $a x^{2} + b x + c = 2$ 无实数解；
④点 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ 在抛物线上，若 $x_{1} + x_{2} > - \frac{1}{2}$ ， $x_{1} > x_{2}$ ，总有 $y_{1} < y_{2}$ ，则 $0 < m \leq \frac{1}{2}$ ．
其中正确的是（填写序号）．

查看试题解析

三、解答题（共7题，共72分）

17. 某校为了落实“五育并举”，提升学生的综合素养．在课外活动中开设了四个兴趣小组：A．插花组：B．跳绳组；C．话剧组；D．书法组．为了解学生对每个兴趣小组的参与情况，随机抽取了部分学生进行调查，并将调查结果绘制成不完整的统计图．
请结合图中信息解答下列问题：

(1)、本次共调查了名学生，并将条形统计图补充完整；

(2)、话剧组所对应扇形的圆心角为度；

(3)、书法组成绩最好的4名学生由3名男生和1名女生构成．从中随机抽取2名参加比赛，请用列表或画树状图的方法，求刚好抽到1名男生与1名女生的概率．

查看试题解析
18. 如图，圆内接四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点 $E$ ， $B D$ 平分 $∠ A B C$ ， $∠ B A C = ∠ A D B$ ．

(1)、求证 $D B$ 平分 $∠ A D C$ ，并求 $∠ B A D$ 的大小；

(2)、过点 $C$ 作 $C F ∥ A D$ 交 $A B$ 的延长线于点 $F$ ．若 $A C = A D$ ， $B F = 2$ ，求此圆半径的长．

查看试题解析
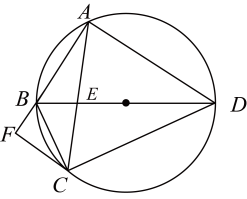19. 如图，二次函数y＝ $\frac{1}{2}$ x²+bx+c的图象与x轴交于A、B两点，与y轴交于点C ，点A的坐标为（﹣1，0），点C的坐标为（0，﹣3），连接BC ．

(1)、求该二次函数的解析式；

(2)、点P是抛物线在第四象限图象上的任意一点，当△BCP的面积最大时，BC边上的高PN的值为．

查看试题解析
20. 如图， $⊙ O$ 的直径 $A B$ 垂直于弦 $D C$ 于点F，点P在 $A B$ 的延长线上， $C P$ 与 $⊙ O$ 相切于点C.

(1)、求证： $∠ P C B = ∠ P A D$ ；

(2)、若 $⊙ O$ 的直径为4，弦 $D C$ 平分半径 $O B$ ，求：图中阴影部分的面积.

查看试题解析
21. 16世纪中叶，我国发明了一种新式火箭“火龙出水”，它是二级火箭的始祖。火箭第一级运行路径形如抛物线，当火箭运行一定水平距离时，自动引发火箭第二级，火箭第二级沿直线运行。
某科技小组运用信息技术模拟火箭运行过程。如图，以发射点为原点，地平线为x轴，垂直于地面的直线为y轴，建立平面直角坐标系，分别得到抛物线 $y = a x^{2} + x$ 和直线 $y = - \frac{1}{2} x + b$ ．其中，当火箭运行的水平距离为9 $k m$ 时，自动引发火箭的第二级．

(1)、若火箭第二级的引发点的高度为3.6 $k m$ ．
①直接写出a ， b的值；
②火箭在运行过程中，有两个位置的高度比火箭运行的最高点低1.35 $k m$ ，求这两个位置之间的距离．

(2)、直接写出a满足什么条件时，火箭落地点与发射点的水平距离超过15 $k m$ ．

查看试题解析
22. 已知四边形 $A B C D$ 内接于 $⊙ O$ ，对角线 $B D$ 是 $⊙ O$ 的直径．

(1)、如图1，连接 $O A ， C A$ ，若 $O A ⊥ B D$ ，求证； $C A$ 平分 $∠ B C D$ ；

(2)、如图2， $E$ 为 $⊙ O$ 内一点，满足 $A E ⊥ B C ， C E ⊥ A B$ ，若 $B D = 3 \sqrt{3}$ ， $A E = 3$ ，求弦 $B C$ 的长．

查看试题解析
23. 课堂上，数学老师组织同学们围绕关于 $x$ 的二次函数 $y = x^{2} + 2 a x + a - 3$ 的最值问题展开探究.
【经典回顾】二次函数求最值的方法.

(1)、老师给出 $a = - 4$ ，求二次函数 $y = x^{2} + 2 a x + a - 3$ 的最小值.
①请你写出对应的函数解析式；
②求当 $x$ 取何值时，函数 $y$ 有最小值，并写出此时的 $y$ 值；
【举一反三】老师给出更多 $a$ 的值，同学们即求出对应的函数在 $x$ 取何值时， $y$ 的最小值. 记录结果，并整理成下表：

$a$

$\dots$
-4
-2
0
2
4

$\dots$

$x$

$\dots$

$*$
2
0
-2
-4

$\dots$
$y$ 的最小值
$\dots$
$*$
-9
-3
-5
-15
$\dots$
注： * 为②的计算结果.
【探究发现】老师： “请同学们结合学过的函数知识，观察表格，谈谈你的发现.”甲同学： “我发现，老师给了 $a$ 值后，我们只要取 $x = - a$ ，就能得到 $y$ 的最小值.”
乙同学： “我发现， $y$ 的最小值随 $a$ 值的变化而变化，当 $a$ 由小变大时， $y$ 的最小值先增大后减小，所以我猜想 $y$ 的最小值中存在最大值 ”

(2)、请结合函数解析式 $y = x^{2} + 2 a x + a - 3$ ，解释甲同学的说法是否合理?

(3)、你认为乙同学的猜想是否正确? 若正确，请求出此最大值；若不正确，说明理由.

查看试题解析

移植总数 $n$	40	150	300	500	700	1000	1500
成活数 $m$	35	134	271	451	631	899	1350
成活的频率 $\frac{m}{n}$	0.875	0.893	0.903	0.902	0.901	0.899	0.900

$a$	$\dots$	-4	-2	0	2	4	$\dots$
$x$	$\dots$	$*$	2	0	-2	-4	$\dots$
$y$ 的最小值	$\dots$	$*$	-9	-3	-5	-15	$\dots$