浙江省温州市永嘉县2017年中考数学三模试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. 下列等式计算正确的是( )A、(﹣2)+3=﹣1 B、3﹣(﹣2)=1 C、(﹣3)+(﹣2)=6 D、(﹣3)+(﹣2)=﹣52. 下列四个几何体中,主视图是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 要使二次根式 有意义,则x应满足( )A、x≠1 B、x≥1 C、x≤1 D、x<14. 抛物线y=x2﹣3x+2与y轴交点的坐标为( )A、(0,2) B、(1,0) C、(2,0) D、(0,﹣3)5. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )
3. 要使二次根式 有意义,则x应满足( )A、x≠1 B、x≥1 C、x≤1 D、x<14. 抛物线y=x2﹣3x+2与y轴交点的坐标为( )A、(0,2) B、(1,0) C、(2,0) D、(0,﹣3)5. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=22°,那么∠2的度数是( )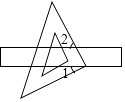 A、22° B、78° C、68° D、70°6. 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=6,DB=3,则 的值为( )
A、22° B、78° C、68° D、70°6. 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=6,DB=3,则 的值为( )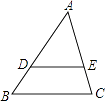 A、 B、 C、 D、27. 四张完全相同的卡片上,分别画有圆、正方形、等边三角形和线段,现从中随机抽取两张,卡片上画的恰好都是中心对称图形的概率为( )A、1 B、 C、 D、8. 某校男子篮球队20名队员的身高如表:则此男子排球队20名队员身高的中位数是( )
A、 B、 C、 D、27. 四张完全相同的卡片上,分别画有圆、正方形、等边三角形和线段,现从中随机抽取两张,卡片上画的恰好都是中心对称图形的概率为( )A、1 B、 C、 D、8. 某校男子篮球队20名队员的身高如表:则此男子排球队20名队员身高的中位数是( )身高(cm)
170
176
178
182
198
人数(个)
4
6
5
3
2
A、176cm B、177cm C、178cm D、180cm9. 某工厂接到加工600件衣服的订单,预计每天做25件,正好按时完成,后因客户要求提前3天交货,工人则需要提高每天的工作效率,设工人每天应多做x件,依题意列方程正确的是( )
A、 ﹣ =3 B、 +3= C、 ﹣ =3 D、 ﹣ =310. 如图,在菱形ABCD中,tan∠ABC= ,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则 的值为( )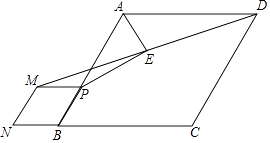 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:m2﹣9=.
12. 有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是 .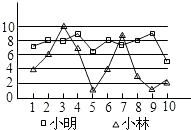 13. 不等式组 的解为 .14. 如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE= .
13. 不等式组 的解为 .14. 如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE= .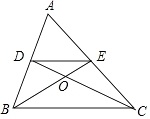 15. 如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转90°得到P′,连CP′,则线段CP′的最小值为 .
15. 如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转90°得到P′,连CP′,则线段CP′的最小值为 .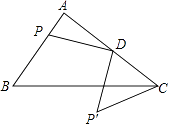 16. 如图,在△ABC中,B、C两点恰好在反比例函数y= (k>0)第一象限的图象上,且BC= ,S△ABC= ,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为 .
16. 如图,在△ABC中,B、C两点恰好在反比例函数y= (k>0)第一象限的图象上,且BC= ,S△ABC= ,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为 .
三、解答题
-
17. 计算题( )﹣1+ +sin30°;
(1)、计算:( )﹣1+ +sin30°;
(2)、先化简,再求值:(m+2)(m﹣2)﹣(m﹣2)2+1,其中m=2.18. 温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:关注情况
频数
频率
A.高度关注
m
0.1
B.一般关注
100
0.5
C.不关注
30
n
D.不知道
50
0.25
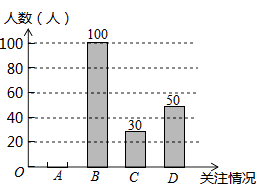 (1)、根据上述统计表可得此次采访的人数为人;m= , n=;
(1)、根据上述统计表可得此次采访的人数为人;m= , n=;
(2)、根据以上信息补全条形统计图;(3)、根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约人.
19. 如图,在方格纸中,线段AB的两个端点都在小方格的格点上,AB=5,请找到一个格点P,连结PA,PB,使得△PAB为等腰三角形(请画出两种,若所画三角形全等,则视为一种).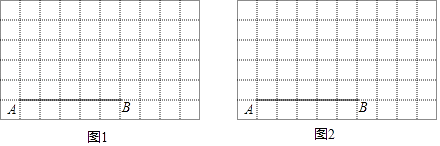 20. 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
20. 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.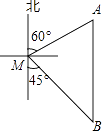 (1)、求渔船从B到A的航行过程中与码头M之间的最小距离.(2)、若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.21. 如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.
(1)、求渔船从B到A的航行过程中与码头M之间的最小距离.(2)、若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.21. 如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.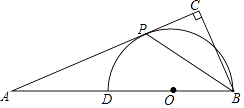 (1)、求证:BP平分∠ABC;(2)、若PC=1,AP=3,求BC的长.22. 温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)、求证:BP平分∠ABC;(2)、若PC=1,AP=3,求BC的长.22. 温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)、若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;(2)、若建成后的寝室可供600人住宿,求单人间的数量;(3)、若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?23. 如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.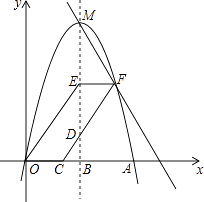 (1)、求a的值及M的坐标;
(1)、求a的值及M的坐标;
(2)、当BD为何值时,点F恰好落在该抛物线上?
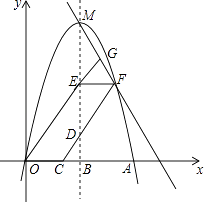
(3)、当∠DCB=45°时:①求直线MF的解析式;
②延长OE交FM于点G,四边形DEGF和四边形OEDC的面积分别记为S1、S2 , 则S1:S2的值为(直接写答案)
 24. 如图,在矩形ABCD中,AD=10,E为AB上一点,且AE= AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.
24. 如图,在矩形ABCD中,AD=10,E为AB上一点,且AE= AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.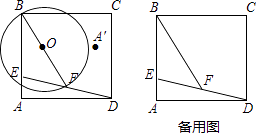 (1)、用a的代数式表示DE2= , BF2=;(2)、求证:⊙O必过BC的中点;(3)、若⊙O与矩形ABCD各边所在的直线相切时,求a的值;(4)、作A关于直线BF的对称点A′,若A′落在矩形ABCD内部(不包括边界),则a的取值范围 . (直接写出答案)
(1)、用a的代数式表示DE2= , BF2=;(2)、求证:⊙O必过BC的中点;(3)、若⊙O与矩形ABCD各边所在的直线相切时,求a的值;(4)、作A关于直线BF的对称点A′,若A′落在矩形ABCD内部(不包括边界),则a的取值范围 . (直接写出答案)