天津市二十九中2017年中考数学模拟试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. 计算(﹣3)﹣(﹣6)的结果等于( )A、3 B、﹣3 C、9 D、182. 如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧 上的一点,则cos∠APB的值是( )
 A、45° B、1 C、 D、无法确定3. 下列图形既是轴对称图形又是中心对称图形的是( )A、
A、45° B、1 C、 D、无法确定3. 下列图形既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 2016年2月19日,经国务院批准,设立无锡市新吴区,将无锡市原新区的鸿山、旺庄、硕放、梅村、新安街道划和滨湖区的江溪街道归新吴区管辖.新吴区现有总人口322819人,这个数据用科学记数法(精确到千位)可表示为( )A、323×103 B、3.22×105 C、3.23×105 D、0.323×1065. 下列几何体的主视图与其他三个不同的是( )A、
4. 2016年2月19日,经国务院批准,设立无锡市新吴区,将无锡市原新区的鸿山、旺庄、硕放、梅村、新安街道划和滨湖区的江溪街道归新吴区管辖.新吴区现有总人口322819人,这个数据用科学记数法(精确到千位)可表示为( )A、323×103 B、3.22×105 C、3.23×105 D、0.323×1065. 下列几何体的主视图与其他三个不同的是( )A、 B、
B、 C、
C、 D、
D、 6. 16的算术平方根和25的平方根的和是( )A、9 B、﹣1 C、9或﹣1 D、﹣9或17. 计算 的正确结果是( )A、0 B、 C、 D、8. 若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2013﹣a﹣b的值是( )A、2 018 B、2 008 C、2 014 D、2 0129. 当实数x的取值使得 有意义时,函数y=x+1中y的取值范围是( )A、y≥﹣3 B、y≥﹣1 C、y>﹣1 D、y≤﹣310. 已知反比例函数y= ,当1<x<2时,y的取值范围是( )A、0<y<5 B、1<y<2 C、5<y<10 D、y>1011. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致为( )
6. 16的算术平方根和25的平方根的和是( )A、9 B、﹣1 C、9或﹣1 D、﹣9或17. 计算 的正确结果是( )A、0 B、 C、 D、8. 若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2013﹣a﹣b的值是( )A、2 018 B、2 008 C、2 014 D、2 0129. 当实数x的取值使得 有意义时,函数y=x+1中y的取值范围是( )A、y≥﹣3 B、y≥﹣1 C、y>﹣1 D、y≤﹣310. 已知反比例函数y= ,当1<x<2时,y的取值范围是( )A、0<y<5 B、1<y<2 C、5<y<10 D、y>1011. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致为( )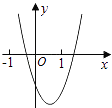 A、
A、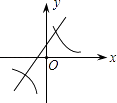 B、
B、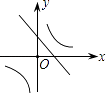 C、
C、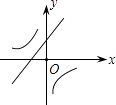 D、
D、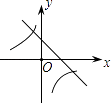
二、填空题:
-
12. 分解因式:x3﹣6x2+9x= .13. 函数y= 的自变量的取值范围是 .14. 某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是 .15. 某地市话的收费标准为:
①通话时间在3分钟以内(包括3分钟)话费0.5元;
②通话时间超过3分钟时,超过部分的话费按每分钟0.15元计算.
在一次通话中,如果通话时间超过3分钟,那么话费y(元)与通话时间x(分)之间的关系式为 .
16. 如图,AD=DF=FB,DE∥FG∥BC,则SⅠ:SⅡ:SⅢ= .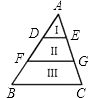 17. 如图,锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D.请写出图中的一对相似三角形,如 .
17. 如图,锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D.请写出图中的一对相似三角形,如 .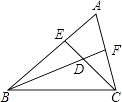
三、解答题:
-
18. 解不等式组 ,并写出该不等式组的整数解.19. 有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.(1)、请用树状图或列表的方法求这三条线段能组成三角形的概率;(2)、求这三条线段能组成直角三角形的概率.20. 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
 (1)、求∠APB的度数;(2)、当OA=3时,求AP的长.21. 如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里.
(1)、求∠APB的度数;(2)、当OA=3时,求AP的长.21. 如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里. (1)、求出此时点A到岛礁C的距离;
(1)、求出此时点A到岛礁C的距离;
(2)、若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
22. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)、若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?(2)、在(1)的条件下,该服装店在6月21日“父亲节”当天对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?23. 在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.(1)、如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积; (2)、如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.
(2)、如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.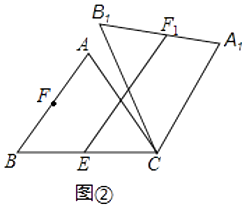 24. 如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
24. 如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K. (1)、将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
(1)、将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①点B的坐标为(、),BK的长是 , CK的长是;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)、将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2 , 在点M的运动过程中,S1•S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.