山东省青岛市莱西市2017年中考数学一模试卷

试卷更新日期：2017-12-07 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{6}$ 的倒数是（）

A、6 B、 $\frac{1}{6}$ C、﹣6 D、﹣ $\frac{1}{6}$

查看试题解析
2. 某小区居民王先生改进用水设施，在5年内帮助他居住小区的居民累计节水39 400吨，将39 400用科学记数法表示为（）

A、3.94×10³ B、3.94×10⁴ C、39.4×10³ D、0.394×10⁵

查看试题解析
3. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、等边三角形 B、平行四边形 C、一次函数图象 D、反比例函数图象

查看试题解析
4. 下列运算正确的是（）

A、（a﹣b）²=a²﹣b² B、（2a+1）（2a﹣1）=4a﹣1 C、（﹣2a³）²=4a⁶ D、x²﹣8x+16=（x+4）²

查看试题解析
5. 如图，面积为6cm²的△ABC纸片沿BC方向平移至△DEF的位置，平移的距离是BC长的2倍，则△ABC纸片扫过的面积为（）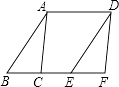

A、18cm² B、21cm² C、27cm² D、30cm²

查看试题解析
6. 某施工队挖掘一条长90米的隧道，开工后每天比原计划多挖1米，结果提前3天完成任务，原计划每天挖多少米？若设原计划每天挖x米，则依题意列出正确的方程为（）

A、 $\frac{90}{x} - \frac{90}{x - 1}$ =3 B、 $\frac{90}{x - 1} - \frac{90}{x} = 3$ C、 $\frac{90}{x} - \frac{90}{x + 1} = 3$ D、 $\frac{90}{x + 1} - \frac{90}{x} = 3$

查看试题解析
7. 如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD，若DE=6，∠BAC+∠EAD=180°，则弦BC的长等于（）

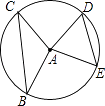A、8 B、10 C、11 D、12

查看试题解析
8. 如图图案是用四种基本图形按照一定规律拼成的，第10个图案中的最下面一行从左至右的第2个基本图形应是（）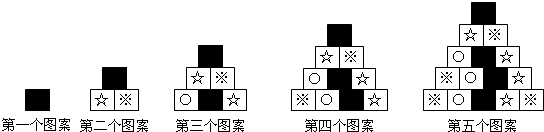

A、 B、 C、 D、

查看试题解析

二、填空题

9. 计算 $(\sqrt{27} - \sqrt{12}) \div \sqrt{3}$ = ．

查看试题解析
10. 如图，大圆半径为6，小圆半径为2，在如图所示的圆形区域中，随机撒一把豆子，多次重复这个实验，若把“豆子落在小圆区域A中”记作事件W，请估计事件W的概率P（W）的值．

查看试题解析
11. 已知点A在反比例函数 $y = \frac{k}{x}$ 的图象上，AB⊥y轴，点C在x轴上，S_△_ABC=2，则反比例函数的解析式为．

查看试题解析
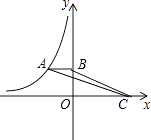12. 如图是某几何体的三视图，根据图中数据，求得该几何体的体积为．

查看试题解析
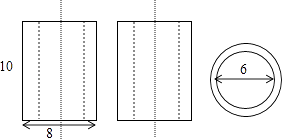13. 如图，在四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DP⊥AB于P．若四边形ABCD的面积是18，则DP的长是．

查看试题解析
14. 小华将一条直角边长为1的一个等腰直角三角形纸片（如图1），沿它的对称轴折叠1次后得到一个等腰直角三角形（如图2），再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形（如图3），则图3中的等腰直角三角形的一条腰长为；同上操作，若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形（如图n+1）的一条腰长为．

查看试题解析

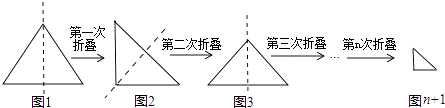
三、作图题

15. 如图，在一块圆形铁板上剪出了一个最大的等边三角形ABC，请你画出原来的圆形铁板．

查看试题解析

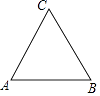
四、解答题

16. 计算：

(1)、化简： $\frac{2 a}{a^{2} - 4} \cdot (\frac{a^{2} + 4}{4 a} - 1)$

(2)、解不等式组，并求其最小整数解． ${\begin{matrix} \frac{x - 3}{2} + 3 \geq x \\ 1 - 3 (x - 1) < 8 - x \end{matrix}$ ．

查看试题解析
17. 某同学报名参加校运动会，有以下5个项目可供选择：
径赛项目：100m，200m，400m（分别用A₁、A₂、A₃表示）；
田赛项目：跳远，跳高（分别用B₁、B₂表示）．
该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率．

查看试题解析
18. 某数学老师为了了解学生在数学学习中常见错误的纠正情况，收集了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对她所任教的初三（1）班和（2）班进行了检测．如图表示从两班各随机抽取的10名学生的得分情况：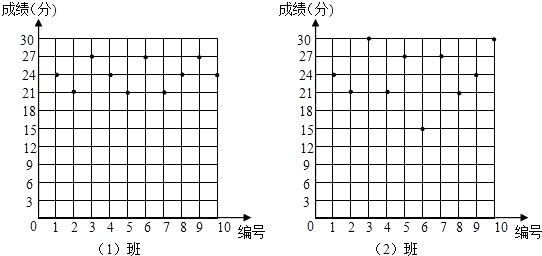

(1)、利用图中提供的信息，补全下表：
班级
平均数（分）
中位数（分）
众数（分）
（1）班
24
24
（2）班
24

(2)、若把24分以上（含24分）记为“优秀”，两班各有60名学生，请估计两班各有多少名学生成绩优秀；

(3)、观察图中的数据分布情况，你认为哪个班的学生纠错的整体情况更好一些？

查看试题解析
19. 如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26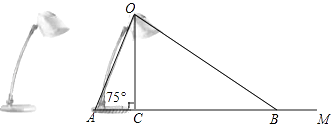， $\sqrt{3} \approx 1.73$ ）．

查看试题解析
20. 为更新果树品种，某果园计划新购进A，B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种树苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．

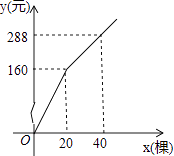(1)、求y与x的函数关系式；

(2)、若在购买计划中，B种树苗的数量不超过35棵，但不少于A种树苗的数量，请设计购买方案，使总费用最低，并求出最低费用．

查看试题解析
21. 如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．

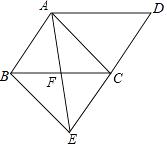(1)、求证：△ABF≌△ECF；

(2)、若∠AFC=2∠D，连接AC、BE．求证：四边形ABEC是矩形．

查看试题解析
22. 如图将小球从斜坡的O点抛出，小球的抛出路线可以用二次函数y=ax²+bx刻画，顶点坐标为（4，8），斜坡可以用 $y = \frac{1}{2} x$ 刻画．

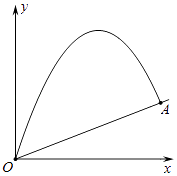(1)、求二次函数解析式；

(2)、若小球的落点是A，求点A的坐标；

(3)、求小球飞行过程中离坡面的最大高度．

查看试题解析

23. 用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形．设格点多边形的面积为S，该多边形各边上的格点个数之和为m，内部的格点个数为n，试探究S与m、n之间的关系式．

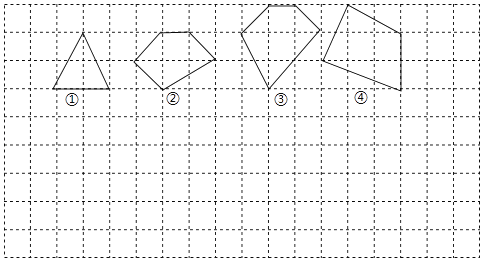(1)、根据图中提供的信息填表：

	格点多边形各边上的格点的个数	格点边多边形内部的格点个数	格点多边形的面积
多边形1	4	1	2
多边形2	5	2	②
多边形3	6	3	5
多边形4	①	4	$\frac{11}{2}$
一般格点多边形	m	n	S

则S=（用含m、n的代数式表示）

(2)、对正三角形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，如图1、2是该正三角形格点中的两个多边形：设格点多边形的面积为S，该多边形各边上的格点个数之和为m，内部的格点个数为n，试探究S与m、n之间的关系式．则S与m、n之间的关系为S=（用含m、n的代数式表示）．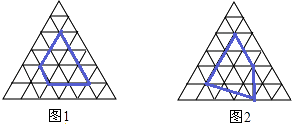

查看试题解析

24. 已知：如图，在Rt△ABC中，∠C=90°，AC=8cm，BC=6cm．直线PE从B点出发，以2cm/s的速度向点A方向运动，并始终与BC平行，与AC交于点E．同时，点F从C点出发，以1cm/s的速度沿CB向点B运动，设运动时间为t （s）（0＜t＜5）．

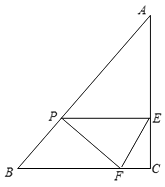(1)、当t为何值时，四边形PFCE是矩形？

(2)、设△PEF的面积为S（cm²），求S与t的函数关系式；

(3)、是否存在某一时刻t，使△PEF的面积是△ABC面积的 $\frac{1}{5}$ ？若存在，求出t的值；若不存在，请说明理由．

(4)、连接BE，是否存在某一时刻t，使PF经过BE的中点？若存在，求出t的值；若不存在，请说明理由．

查看试题解析

班级	平均数（分）	中位数（分）	众数（分）
（1）班		24	24
（2）班	24