陕西省西安市2017年中考数学模拟试卷

试卷更新日期：2017-12-07 类型：中考模拟

进入出卷网下载

一、选择题

1. $\sqrt{2}$ 的相反数是（）

A、﹣ $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、﹣ $\frac{\sqrt{2}}{2}$ D、1.414

查看试题解析
2. 下列几何体中，左视图与主视图相同的是（）

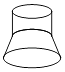A、 B、 C、 D、

查看试题解析
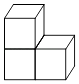3. 下列计算正确的是（）

A、（﹣3a²b）³=﹣3a⁵b³ B、 $\frac{1}{2}$ ab²•（﹣4a³b）=﹣2a⁴b³ C、4m³n²÷m³n²=0 D、a⁵﹣a²=a³

查看试题解析
4. 如图，直线a、b被c所截，若a∥b，∠1=45°，∠3=100°，则∠2的度数为（）

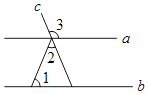A、70° B、65° C、60° D、55°

查看试题解析
5. 如果y=（1﹣m）x $^{m^{2} - 2}$ 是正比例函数，且y随x的增大而减小，则m的值为（）

A、m=﹣ $\sqrt{3}$ B、m= $\sqrt{3}$ C、m=3 D、m=﹣3

查看试题解析
6. 如图，已知△ABC中，AB=10，AC=8，BC=6，DE是AC的垂直平分线，DE交AB于点D，交AC于点E，连接CD，则CD=（）

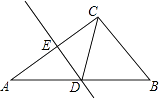A、3 B、4 C、4.8 D、5

查看试题解析
7. 如图，1﹣4月份，甲、乙两工厂月生产增长量的变化情况，则甲工厂和乙工厂生产增长量差值最大的月份是（）

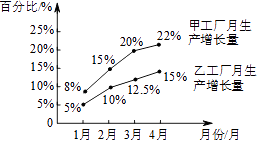A、1月份 B、2月份 C、3月份 D、4月份

查看试题解析
8. 已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交，且函数值y随自变量x的增大而增大，则k，b的取值情况为（）

A、k＞1，b＜0 B、k＞1，b＞0 C、k＞0，b＞0 D、k＞0，b＜0

查看试题解析
9. 如图，在矩形ABCD中，AB=4，BC=6，将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF，延长DA交FG于点H，则GH的长为（）

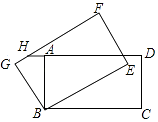A、8﹣4 $\sqrt{3}$ B、 $\frac{8 \sqrt{3}}{3}$ ﹣4 C、3 $\sqrt{3}$ ﹣4 D、6﹣3 $\sqrt{3}$

查看试题解析
10. 如图是抛物线y=ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间．则下列结论：
①a﹣b+c＞0；
②3a+b=0；
③b²=4a（c﹣n）；
④一元二次方程ax²+bx+c=n﹣1有两个不相等的实数根．
其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. ﹣1³+ $\sqrt{4}$ ﹣12sin30°= ．

查看试题解析
12. 正三角形的边长为4，则它的面积为
31+2sin18°≈（保留两位小数）

查看试题解析
13. 如图所示，直线y=kx（k＜0）与双曲线y=﹣ $\frac{2}{x}$ 交于M（x₁ ， y₁），N（x₂ ， y₂）两点，则 $\frac{3}{5}$ x₁y₂﹣3x₂y₁的值为．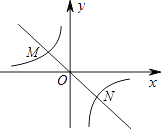

查看试题解析
14. 如图，在Rt△ABC中，∠C=90°，AB=13，AC=12，经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N，则线段MN长度的最小值为．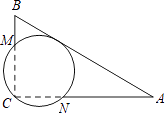

查看试题解析

三、解答题

15. 1^﹣¹﹣2sin30°+|3.14﹣π|+（ $\frac{\sqrt{2}}{2}$ ﹣1）⁰ ．

查看试题解析
16. 解方程： $\frac{3}{x^{2} - 1}$ ﹣ $\frac{x}{x + 1}$ =1．

查看试题解析
17. 如图，已知锐角三角形ABC，求作⊙C，使⊙C与AB所在的直线相切于点D（保留作图痕迹，不写作法）．

查看试题解析
18. 某校为了了解七年级学生课外活动情况，随机调查了该校若干名学生，调查他们喜欢各类课外活动的情况（课外活动分为四类：A﹣﹣喜欢打乒乓球的人，B﹣﹣喜欢踢足球的人，C﹣﹣喜欢打篮球的人，D﹣﹣喜欢其他的人），并将调查结果绘制成如下两幅不完整的统计图．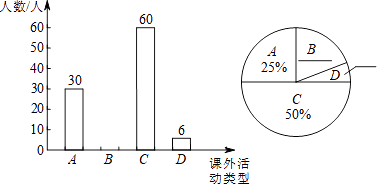
根据统计图信息完成下列问题：

(1)、调查的学生人数为人．

(2)、补全条形统计图和扇形统计图．

(3)、若该校七年级共有600人，请估计七年级学生中喜欢打乒乓球的人数．

查看试题解析
19. 已知：如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE=CF，作EG∥FH，分别与对角线BD交于点G、H，连接EH，FG．

(1)、求证：△BFH≌△DEG；

(2)、连接DF，若BF=DF，则四边形EGFH是什么特殊四边形？证明你的结论．

查看试题解析
20. 已知某山区的平均气温与该山的海拔高度的关系见下表：
海拔高度（单位：米）
0
100
200
300
400
…
平均气温（单位：℃）
22
21.5
21
20.5
20
…

(1)、若海拔高度用x（米）表示，平均气温用y（℃）表示，试写出y与x之间的函数关系式；

(2)、若某种植物适宜生长在18℃～20℃（包含18℃，也包含20℃）山区，请问该植物适宜种植在海拔为多少米的山区？

查看试题解析
21. 如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB，标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，求建筑物的高．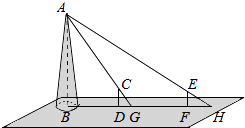

查看试题解析
22. “五一”小长假期间，某超市为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”、“30元”的字样．规定：顾客在本超市一次性购物满500元以上均可获得两次摸球的机会（摸出小球后放回）．超市根据两小球所标金额的和返还相应的代金券．

(1)、顾客甲购物1000元，则他最少可获元代金券，最多可获元代金券．

(2)、请用树形图或列表方法，求出顾客甲获得不低于30元（含30元）代金券的概率．

查看试题解析
23. 已知：如图，在△ABC中，D是AB边上一点，圆O过D、B、C三点，∠DOC=2∠ACD=90°．

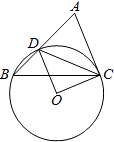(1)、求证：直线AC是圆O的切线；

(2)、如果∠ACB=75°，圆O的半径为2，求BD的长．

查看试题解析
24. 已知抛物线y=3ax²+2bx+c，
（Ⅰ）若a=b=1，c=﹣1，求该抛物线与x轴公共点的坐标；
（Ⅱ）若a=b=1，且当﹣1＜x＜1时，抛物线与x轴有且只有一个公共点，求c的取值范围；
（Ⅲ）若a+b+c=0，且x₁=0时，对应的y₁＞0；x₂=1时，对应的y₂＞0，试判断当0＜x＜1时，抛物线与x轴是否有公共点？若有，请证明你的结论；若没有，阐述理由．

查看试题解析
25. 问题探究

(1)、请在图①的正方形ABCD的对角线BD上作一点P，使PA+PC最小；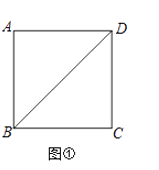

(2)、如图②，点P为矩形ABCD的对角线BD上一动点，AB=2，BC=2 $\sqrt{3}$ ，点E为BC边的中点，求作一点P，使PE+PC最小，并求这个最小值．

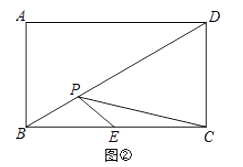(3)、如图③，李师傅有一块边长为1000米的菱形ABCD采摘园，AC=1200米，BD为小路，BC的中点E为一水池，李师傅现在准备在小路BD上建一个游客临时休息纳凉室P，为了节省土地，使休息纳凉室P到水池E与大门C的距离之和最短，那么是否存在符合条件的点P？若存在，请作出的点P位置，并求出这个最短距离；若不存在，请说明理由．

查看试题解析

海拔高度（单位：米）	0	100	200	300	400	…
平均气温（单位：℃）	22	21.5	21	20.5	20	…