人教版数学九年级全册知识点训练营——反比例函数的解题模型
试卷更新日期:2024-10-30 类型:复习试卷
一、一点一垂线型
-
1. 如图, 点 在反比例函数 的图象上, 且点 的横坐标为 轴于点 . 若 的面积是 3 , 则 的值是( )
 A、3 B、6 C、-3 D、-62. 如图,P是反比例函数 的图象上任意一点,过点 P作PM⊥x轴,垂足为 M.若△POM 的面积等于2,则k的值等于 ( )
A、3 B、6 C、-3 D、-62. 如图,P是反比例函数 的图象上任意一点,过点 P作PM⊥x轴,垂足为 M.若△POM 的面积等于2,则k的值等于 ( ) A、-4 B、4 C、-2 D、23. 如图,在平面直角坐标系中,菱形的对角线在x轴上,顶点A在反比例函数的图象上,则菱形的面积为.
A、-4 B、4 C、-2 D、23. 如图,在平面直角坐标系中,菱形的对角线在x轴上,顶点A在反比例函数的图象上,则菱形的面积为. 4. 如图,的顶点在反比例函数的图象上,顶点在反比例函数的图象上,轴,且的对角线交点为坐标原点.若 , 则.
4. 如图,的顶点在反比例函数的图象上,顶点在反比例函数的图象上,轴,且的对角线交点为坐标原点.若 , 则.
二、一点两垂线型
-
5. 反比例函数的图象如图所示,下列说法正确的是( )
 A、 B、y随x的增大而减小 C、若矩形的面积为2,则 D、若图象上点B的坐标是 , 则当时,y的取值范围是6. 如图,点M是反比例函数y=(a≠0)的图象上一点,过M点作x轴、y轴的平行线,若S阴影=8,则此反比例函数解析式为
A、 B、y随x的增大而减小 C、若矩形的面积为2,则 D、若图象上点B的坐标是 , 则当时,y的取值范围是6. 如图,点M是反比例函数y=(a≠0)的图象上一点,过M点作x轴、y轴的平行线,若S阴影=8,则此反比例函数解析式为 7. 如图,平行四边形 的顶点 在反比例函数 的图象上,点 在 轴正半轴上,点 在 轴上, 与 轴交于点 ,若 ,则 的值为( )
7. 如图,平行四边形 的顶点 在反比例函数 的图象上,点 在 轴正半轴上,点 在 轴上, 与 轴交于点 ,若 ,则 的值为( ) A、 B、 C、 D、128. 如图,D为反比例函数 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
A、 B、 C、 D、128. 如图,D为反比例函数 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.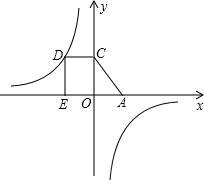
三、两点一垂线型
-
9. 如图直线y=mx与双曲线y= 交于点A、B , 过A作AM⊥x轴于M点,连接BM , 若S△AMB=2,则k的值是( )
 A、1 B、2 C、3 D、410. 如图,过原点O的直线与反比例函数的图像交于点A、P,过点P作x轴的垂线,点B为垂足,连接 , 若的面积是5,则 .
A、1 B、2 C、3 D、410. 如图,过原点O的直线与反比例函数的图像交于点A、P,过点P作x轴的垂线,点B为垂足,连接 , 若的面积是5,则 . 11. 已知:如图所示,反比例函数 的图象与正比例函数 的图象交于A、B,作AC⊥ 轴于C,连BC,则△ABC的面积为3,求反比例函数的解析式.
11. 已知:如图所示,反比例函数 的图象与正比例函数 的图象交于A、B,作AC⊥ 轴于C,连BC,则△ABC的面积为3,求反比例函数的解析式.
四、两点两垂线型
-
12. 如图, 在▱ABCD中, AB∥x轴, 点B、D在反比例函数. 的图象上,若▱ABCD的面积是8, 则k的值是 ( )
 A、2 B、4 C、6 D、813. 如图,函数y=-x与函数y=-的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D,则四边形ACBD的面积 .
A、2 B、4 C、6 D、813. 如图,函数y=-x与函数y=-的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D,则四边形ACBD的面积 .
五、两点和原点型
-
14. 如图,矩形OABC的顶点A,C分别在y轴、x轴的正半轴上,D 为AB 的中点,反比例函数的图象经过点 D,且与BC边相交于点E,连结OD,OE,DE.若△ODE的面积为3,则k的值为.
 15. 如图,已知一次函数的图象与反比例函数的图像交于、两点,点的坐标是 , 点的坐标是 .
15. 如图,已知一次函数的图象与反比例函数的图像交于、两点,点的坐标是 , 点的坐标是 . (1)、求出两个函数解析式;(2)、求出的面积;(3)、直接写出满足的的取值范围.16. 如图,已知点A的坐标为 , 将线段OA向左平移6个单位长度,再向上平移个单位长度可得到线段CB .
(1)、求出两个函数解析式;(2)、求出的面积;(3)、直接写出满足的的取值范围.16. 如图,已知点A的坐标为 , 将线段OA向左平移6个单位长度,再向上平移个单位长度可得到线段CB . (1)、点C的坐标为 , 点B的坐标为(均用含m的式子表示)(2)、若点B , C同时落在反比例函数的图象上.
(1)、点C的坐标为 , 点B的坐标为(均用含m的式子表示)(2)、若点B , C同时落在反比例函数的图象上.①求m及k的值;
②求的面积
17. 某兴趣小组利用代数推理方法发现了反比例函数一个有趣的结论.小龙:如图1,直线与双曲线交于两点,根据中心对称性可以得到 .
 (1)、【轻松探究】
(1)、【轻松探究】直线与双曲线交于两点,与轴分别交于点 , 试证明: .
请完整的写出上述推理过程.小华:如图2,直线与双曲线联立可得 , 进而求得与的值,由 , 证得线段的中点与线段的中点重合即可.
(2)、【深入探究】直线与双曲线交于两点,与轴分别交于点 , , 试问:还成立吗?请说明理由.
(3)、【模型应用】如图3,直线与双曲线交于两点,与轴分别交于点 . 连接 . 若的面积为 , 求的值.
六、两曲一平行型


