山东省临沂市郯城县2017年中考数学一模试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. 实数﹣2015的绝对值是( )A、2015 B、﹣2015 C、±2015 D、2. 移动互联网已经全面进入人们的日常生活.截至2015年3月,全国4G用户总数达到1.62亿,其中1.62亿用科学记数法表示为( )A、1.62×104 B、1.62×106 C、1.62×108 D、0.162×1093. 下列式子中正确的是( )A、( )﹣2=﹣9 B、(﹣2)3=﹣6 C、 =﹣2 D、(﹣3)0=14. 将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
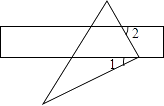 A、30° B、45° C、60° D、65°5. 已知x= ,y= ,则x2+xy+y2的值为( )A、2 B、4 C、5 D、76. 不等式组 的整数解的个数是( )A、3 B、5 C、7 D、无数个7. 化简 的结果是( )A、x+1 B、 C、x﹣1 D、8. 若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是( )A、6cm B、9cm C、12cm D、18cm9. 如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 的线段的概率为( )
A、30° B、45° C、60° D、65°5. 已知x= ,y= ,则x2+xy+y2的值为( )A、2 B、4 C、5 D、76. 不等式组 的整数解的个数是( )A、3 B、5 C、7 D、无数个7. 化简 的结果是( )A、x+1 B、 C、x﹣1 D、8. 若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是( )A、6cm B、9cm C、12cm D、18cm9. 如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 的线段的概率为( )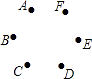 A、 B、 C、 D、10. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
A、 B、 C、 D、10. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( ) A、 B、 C、 D、11. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y= 与正方形ABCD有公共点,则k的取值范围为( )
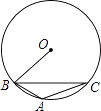
A、 B、 C、 D、11. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y= 与正方形ABCD有公共点,则k的取值范围为( ) A、1<k<9 B、2≤k≤34 C、1≤k≤16 D、4≤k<1612.
A、1<k<9 B、2≤k≤34 C、1≤k≤16 D、4≤k<1612.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
 A、80° B、100° C、110° D、130°13. 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )
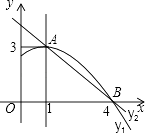
A、80° B、100° C、110° D、130°13. 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( ) A、 B、 C、 D、14. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
A、 B、 C、 D、14. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(﹣1,0);
⑤当1<x<4时,有y2<y1 ,
其中正确的是( )
 A、①②③ B、①③④ C、①③⑤ D、②④⑤
A、①②③ B、①③④ C、①③⑤ D、②④⑤二、填空题
-
15. 分解因式:5x3﹣10x2+5x= .16. 分式方程 的解为 .17. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是 . (请写出正确结论的序号).
 18. 如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点,如运动的路径是最短的,则AC的长为
18. 如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点,如运动的路径是最短的,则AC的长为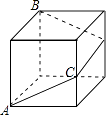 19. 读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 ,这里“∑”是求和符号,通过对以上材料的阅读,计算 = .
19. 读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 ,这里“∑”是求和符号,通过对以上材料的阅读,计算 = .三、解答题
-
20. 计算:﹣32÷ × +| ﹣3|21. 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
请根据图表信息解答下列问题:
 (1)、a=;(2)、补全条形统计图;(3)、据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.22. 如图,在▱ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
(1)、a=;(2)、补全条形统计图;(3)、据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.22. 如图,在▱ABCD中,E、F分别是AB、DC边上的点,且AE=CF, (1)、求证:△ADE≌△CBF.(2)、若∠DEB=90°,求证:四边形DEBF是矩形.23. 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)、求证:△ADE≌△CBF.(2)、若∠DEB=90°,求证:四边形DEBF是矩形.23. 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D. (1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若AC=3,∠B=30°.
(1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若AC=3,∠B=30°.①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
24. 我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元. (1)、求W关于x的函数关系式,并写出自变量x的取值范围;(2)、若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;(3)、“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,甲乙两团队联合购票比分别购票最多节约3400元,求a的值.
(1)、求W关于x的函数关系式,并写出自变量x的取值范围;(2)、若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;(3)、“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,甲乙两团队联合购票比分别购票最多节约3400元,求a的值.
25. 在△ABC中,AB=AC=5,cos∠ABC= ,将△ABC绕点C顺时针旋转,得到△A1B1C.(1)、如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;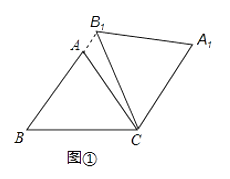 (2)、如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.
(2)、如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.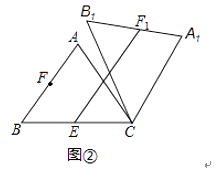 26. 已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.(1)、如图1,若该抛物线经过原点O,且a=﹣ .
26. 已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.(1)、如图1,若该抛物线经过原点O,且a=﹣ .①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
 (2)、如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是4个,请直接写出a的取值范围.
(2)、如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是4个,请直接写出a的取值范围.