山东省临沂市费县2017年中考数学二模试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. ﹣3的倒数的绝对值是( )A、﹣3 B、﹣ C、 D、32. 2016年山东省高考报名人数位居全国第三,约有696000人报名,将696000用科学记数法表示为( )A、69.6×104 B、6.96×105 C、6.96×106 D、0.696×1063. 下列计算中,正确的是( )A、(a3)4=a12 B、a3•a5=a15 C、a2+a2=a4 D、a6÷a2=a34. 如图,直线a∥b,直线c分别与a、b相交于A,B两点,AC⊥AB于点A,交直线b于点C.已知∠1=44°,则∠2的度数是( )
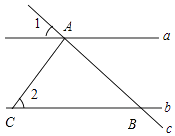 A、36° B、44° C、46° D、56°5. 某学校为了了解九年级女生仰卧起坐训练情况,课外活动时间随机抽取10名女生测试,成绩如下表所示,那么这10名女生测试成绩的众数与中位数依次是( )
A、36° B、44° C、46° D、56°5. 某学校为了了解九年级女生仰卧起坐训练情况,课外活动时间随机抽取10名女生测试,成绩如下表所示,那么这10名女生测试成绩的众数与中位数依次是( )女生编号
1
2
3
4
5
6
7
8
9
10
成绩/个
48
49
52
47
51
53
52
49
51
49
A、52,51 B、51,51 C、49,49 D、49,506. 不等式 的解集在数轴上表示正确的是( )A、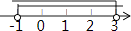 B、
B、 C、
C、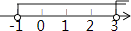 D、
D、 7. 化简 ﹣ 等于( )A、 B、 C、﹣ D、﹣8. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 ﹣ =20 B、 ﹣ =20 C、 ﹣ = D、 ﹣ =9. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x﹣3|,则其结果恰为2的概率是( )
7. 化简 ﹣ 等于( )A、 B、 C、﹣ D、﹣8. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 ﹣ =20 B、 ﹣ =20 C、 ﹣ = D、 ﹣ =9. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x﹣3|,则其结果恰为2的概率是( )
A、 B、 C、 D、10. 如图是某工件的三视图,则此工件的表面积为( ) A、15πcm2 B、51πcm2 C、66πcm2 D、24πcm211. 已知抛物线y=x2﹣x﹣3与x轴的一个交点为(m,0),则代数式m2﹣m+2017的值为( )A、2017 B、2020 C、2019 D、201812. 观察下列等式:
A、15πcm2 B、51πcm2 C、66πcm2 D、24πcm211. 已知抛物线y=x2﹣x﹣3与x轴的一个交点为(m,0),则代数式m2﹣m+2017的值为( )A、2017 B、2020 C、2019 D、201812. 观察下列等式:第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
A、41 B、45 C、43 D、4413. 如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )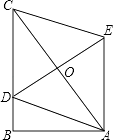 A、5 B、6 C、12 D、1314. 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A、5 B、6 C、12 D、1314. 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( ) A、
A、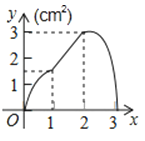 B、
B、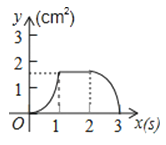 C、
C、 D、
D、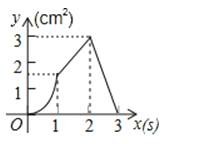
二、填空题
-
15. 因式分解:3x2﹣6x+3= .16. 当x满足x﹣4=0时,( )÷ = .17. 已知,在平行四边形ABCD中,点E在直线AD上,AE= AD,连接CE交BD于点F,则EF:FC的值是 .18. 如图,反比例函数y= 的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为 .
 19. 我们根据指数运算,得出了一种新的运算.下表是两种运算对应关系的一组实例:根据上表规律,某同学写出了三个式子,①log232=5;②log416=4;③log2 =﹣1,其中正确的是(填式子序号)
19. 我们根据指数运算,得出了一种新的运算.下表是两种运算对应关系的一组实例:根据上表规律,某同学写出了三个式子,①log232=5;②log416=4;③log2 =﹣1,其中正确的是(填式子序号)指数运算
22=2
22=4
23=8
…
31=3
32=9
33=27
…
新运算
log22=1
log24=2
log28=3
…
log33=1
log39=2
log327=3
…
三、解答题
-
20. 计算:2cos30°+(π﹣4)0﹣ +|1﹣ |+( )﹣1 .21. 某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
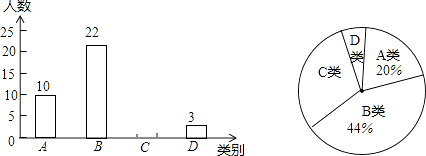 (1)、本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;(2)、请补全统计图;(3)、若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?22. 如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据 ≈1.41, ≈1.73).
(1)、本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;(2)、请补全统计图;(3)、若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?22. 如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据 ≈1.41, ≈1.73).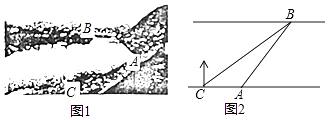 23. 如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.、
23. 如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.、 (1)、求证:CE是⊙O的切线;(2)、若∠D=30°,BD=4,求⊙O的半径r.24. 某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
(1)、求证:CE是⊙O的切线;(2)、若∠D=30°,BD=4,求⊙O的半径r.24. 某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:x(元)
200
240
270
300
y(间)
90
70
55
40
(1)、求y与x之间的函数表达式;(2)、已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)25. 已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.(1)、如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;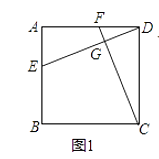 (2)、如图2,若四边形ABCD是矩形,且DE⊥CF,求证: = ;
(2)、如图2,若四边形ABCD是矩形,且DE⊥CF,求证: = ;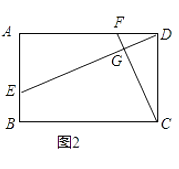 (3)、如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.
(3)、如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.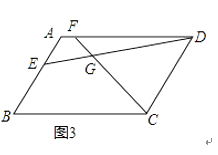 26. 如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣ x2+bx+c经过点A、C,与AB交于点D.
26. 如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣ x2+bx+c经过点A、C,与AB交于点D.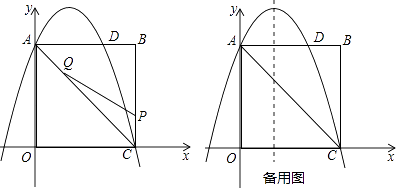 (1)、求抛物线的函数解析式;(2)、点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
(1)、求抛物线的函数解析式;(2)、点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣ x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.