【提升版】浙教版数学八上5.4 一次函数的图象与性质同步练习
试卷更新日期:2024-10-29 类型:同步测试
一、选择题
-
1. 一次函数y=kx+k(k<0)的图象大致是( )A、
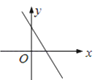 B、
B、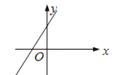 C、
C、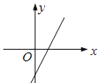 D、
D、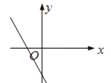 2. 对于一次函数y=-x-2,下列说法不正确的是( )A、图象不经过第一象限 B、图象与y轴的交点坐标为(0,-2) C、图象可由直线y=-x向下平移2个单位长度得到 D、若点(1,y1),(4,y2)在一次函数y=-x-2的图象上,则y1<y23. 若一次函数y=(2m﹣3)x﹣1+m的图象不经过第三象限,则m的取值范围是( )A、1<m< B、1≤m< C、1<m≤ D、1≤m≤4. 小明所在学校离家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离S(千米)与所用时间t(分钟)之间的关系( )A、
2. 对于一次函数y=-x-2,下列说法不正确的是( )A、图象不经过第一象限 B、图象与y轴的交点坐标为(0,-2) C、图象可由直线y=-x向下平移2个单位长度得到 D、若点(1,y1),(4,y2)在一次函数y=-x-2的图象上,则y1<y23. 若一次函数y=(2m﹣3)x﹣1+m的图象不经过第三象限,则m的取值范围是( )A、1<m< B、1≤m< C、1<m≤ D、1≤m≤4. 小明所在学校离家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离S(千米)与所用时间t(分钟)之间的关系( )A、 B、
B、 C、
C、 D、
D、 5. 如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
5. 如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 已知点均在一次函数的图象上,则下列说法正确的是( )A、函数图象经过二、三、四象限 B、点在第二象限 C、 D、与x轴的交点坐标为7. 在平面直角坐标系中,为坐标原点,将直线的图像向右平移5个单位长度得到的新的直线分别交轴、轴于、两点,若点( , 都是整数)在内部(不包括边界),则点的个数是( )个A、7 B、8 C、9 D、108. 如图,函数y=﹣x+2图象与x轴、y轴分别交于A、B两点,C(1,0),点P为直线AB上动点,连接OP、PC , 则△OPC的周长最小值为( )
6. 已知点均在一次函数的图象上,则下列说法正确的是( )A、函数图象经过二、三、四象限 B、点在第二象限 C、 D、与x轴的交点坐标为7. 在平面直角坐标系中,为坐标原点,将直线的图像向右平移5个单位长度得到的新的直线分别交轴、轴于、两点,若点( , 都是整数)在内部(不包括边界),则点的个数是( )个A、7 B、8 C、9 D、108. 如图,函数y=﹣x+2图象与x轴、y轴分别交于A、B两点,C(1,0),点P为直线AB上动点,连接OP、PC , 则△OPC的周长最小值为( ) A、3 B、4 C、 D、
A、3 B、4 C、 D、二、填空题
-
9. 在平面直角坐标系中,将直线向左平移个单位长度,得到直线 , 则 .10. 若点 , 都在直线上,则与的大小关系是: .11. 平面直角坐标系xOy中,已知A(3,0),B(0,3).直线y=kx+b(k , b为常数,且k>0)经过点(1,0),并把△AOB分成两部分,其中靠近原点部分的面积为 , 则k的值为 .12. 如果关于的分式方程有非负整数解,一次函数的图象过一、三、四象限,则所有符合条件的整数的和是 .
三、解答题
-
13. 已知一次函数的图象过点 ,
 (1)、求出函数解析式.(2)、求出图象与坐标轴围成的三角形面积.(3)、当取何值时,?14. 如图直线:经过点 , .
(1)、求出函数解析式.(2)、求出图象与坐标轴围成的三角形面积.(3)、当取何值时,?14. 如图直线:经过点 , . (1)、求直线的表达式;(2)、若直线与直线相交于点 , 求点的坐标;(3)、根据图象,直接写出关于的不等式的解集.
(1)、求直线的表达式;(2)、若直线与直线相交于点 , 求点的坐标;(3)、根据图象,直接写出关于的不等式的解集.四、综合题

