【培优版】浙教版数学八上5.4 一次函数的图象与性质同步练习

试卷更新日期：2024-10-29 类型：同步测试

进入出卷网下载

一、选择题

1. 已知直线 $l_{1}$ ： $y = - k x + b$ 与直线 $l_{2}$ ： $y = 3 k x - b$ 在同一平面直角坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在平面直角坐标系中，线段AB的端点 $A (- 1, - 2)$ ， $B (3, - 1)$ ．若直线 $y = k x + 2$ 与线段AB有交点，则k的值可能是（）

A、2 B、3 C、 $- \frac{1}{2}$ D、 $- 4$

查看试题解析
3. 已知点 $M (6, a - 3)$ ， $N (- 2, a)$ ， $P (2, a)$ 在同一个函数图象上，则这个函数图象可能是（）

A、 B、 C、 D、

查看试题解析
4. 定义：平面直角坐标系中，若点A到x轴、y轴的距离和为2，则称点A为“和二点”．例如：点 $B (- 1.2, 0.8)$ 到x轴、y轴距离和为2，则点B是“和二点”，点 $C (1 ， 1), D (- 0.5 ， - 1.5)$ 也是“和二点”．一次函数 $y = k x + b (k \neq 0)$ 的图象l经过点 $E (- 3, - 4)$ ，且图象l上存在“和二点”，则k的取值范围为（）

A、 $\frac{2}{3} \leq k \leq 2$ B、 $\frac{4}{5} \leq k \leq 2$ C、 $\frac{4}{5} \leq k \leq 4$ D、 $\frac{2}{3} \leq k \leq 4$

查看试题解析
5. 关于x的一次函数 $y = \frac{1}{k} (x - 2) + k (1 - x) (0 < k < 1)$ ，当 $2 \leq x \leq 3$ 时，y的最大值是（）

A、 $\frac{1}{k} - 2 k$ B、 $\frac{1}{k} - k$ C、 $2 k$ D、 $\frac{2}{k}$

查看试题解析
6. 直线y＝x+n与直线y＝mx+3n（m是常数，m≠0且m≠1）交于点A ，当n的值发生变化时，点A到直线y＝ $\frac{3}{4}$ x-3的距离总是一个定值，则m的值是（　　）

A、3 B、2 C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 定义一种新运算： $a \oplus b = \{\begin{array}{l} a + b (a \geq b) \\ a - b + 2 (a < b) \end{array}$ ，例如： $3 \oplus 1 = 3 + 1 = 4$ ， $3 \oplus 4 = 3 - 4 + 2 = 1$ ，给出下列说法：
① $(- 4) \oplus (- 5) = - 9$ ；
②若 $3 \oplus (x - 1) = 2$ ，则 $x = 0$ 或4；
③ $(- 7) \oplus (- 2 x + 1) \leq 0$ 的解集为 $x \leq 3$ 或 $x \geq 4$ ；
④若函数 $y = (- x + 6) \oplus (x - 4)$ 的图象与直线 $y = m$ （m为常数）只有1个交点，则 $m < 2$ ．
以上说法中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

8. 在平面直角坐标系xOy中，函数 $y = k x + b (k \neq 0)$ 的图象经过点 $A (0, - 1)$ 和 $B (4, 3)$ ，与过点 $(0, - 3)$ 且平行于x轴的直线交于点C ，当 $x > - 2$ 时，对于x的每一个值，函数 $y = m x (m \neq 0)$ 的值大于函数 $y = k x + b (k \neq 0)$ 的值，写出m的取值范围

查看试题解析
9. 如图，直线y＝3x+6交坐标轴于A、B两点，C为AB中点，点D为AO上一动点，点E在x轴正半轴上，且满足OE＝OD+OB ，则 $\sqrt{2} C D + D E$ 的最小值为．

查看试题解析
10. 已知，一次函数 $y = - \frac{3}{4} x + 6$ 的图象与x轴、y轴分别交于点A、点B，在第一象限内有一点P，使得 $△ A B P$ 是等腰直角三角形，则点P的横坐标为.

查看试题解析
11. 定义：在平面直角坐标系 $x O y$ 中，若点M关于直线 $x = m$ 的对称点 $M^{'}$ 在 $▱ A B C D$ 的内部（不包含边界），则称点M是 $▱ A B C D$ 关于直线 $x = m$ 的“伴随点”．如图，已知 $A (- 2 ， 0) ， B (3 ， 0) ， C (4 ， 4)$ 三点，连接 $B C$ ，以 $A B ， B C$ 为边作 $▱ A B C D$ ．若在直线 $y = x + n$ 上存在点N，使得点N是 $▱ A B C D$ 关于直线 $x = 2$ 的“伴随点”，则n的取值范围是．

查看试题解析

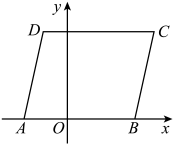
三、解答题

12. 在平面直角坐标系 $x O y$ 中，直线 $y = 2 x$ 上有一点 A，其横坐标为 1 ，经过点 $A$ 的直线交 $x$ 轴负半轴于一点 $P$ ，且 $O P = 3$ ，

(1)、求 $△ O A P$ 的面积；

(2)、求经过点 $P$ 且平分 $△ O A P$ 面积的直线解析式.

查看试题解析
13. 如图，直线AB与x轴、y轴分别交于点A、B ，已知A(6，0)，B(0，4)．

(1)、求直线AB的函数解析式；

(2)、若点C在坐标轴上，且 $S_{Δ A B C}^{} = 18$ ，求点C的坐标；

(3)、点P在第一象限内，且纵坐标为4．若点P关于直线AB的对称点 $P^{'}$ 恰好落在x轴的正半轴上，P $P^{'}$ 与AB相交于点Q ，求点的坐标．

查看试题解析

四、实践探究题

14. 定义：函数图象上到两坐标轴的距离都不大于 $n (n \geq 0)$ 的点叫做这个函数图象的“n级限距点”．例如，点 $(\frac{1}{3} ， \frac{1}{3})$ 是函数 $y = x$ 图象的“ $\frac{1}{2}$ 级限距点”；点 $(2 ， 1)$ 是函数 $y = - \frac{1}{2} x + 2$ 图象的“2级限距点”．

(1)、在① $(- \frac{1}{2} ， - 1)$ ；② $(- \frac{1}{3} ， - \frac{2}{3})$ ；③ $(1 ， 2)$ 三点中，是函数 $y = 2 x$ 图象的“1级限距点”的有（填序号）；

(2)、若y关于x的一次函数 $y = k x + 3$ 图象的“2级限距点”有且只有一个，求k的值；

(3)、若y关于x的函数 $y = - | x - \frac{n}{2} | - 2 n + 1$ 图象存在“n级限距点”，求出n的取值范围．

查看试题解析
15.

(1)、问题发现：
如图1，等腰直角 $△ A O B$ 置于平面直角坐标系中，点 $A$ ， $B$ 的坐标分别为 $(4 ， 0)$ ， $(0 ， 4)$ ， $D$ 是 $A B$ 上一点， $A D = O A$ ，则点 $D$ 的坐标为

(2)、问题探究：如图2，若点 $A$ ， $B$ 的坐标分别为 $(16 ， 0)$ ， $(0 ， 12)$ ，其余条件与（1）相同，求经过 $O$ ， $D$ 两点的直线表达式。

(3)、问题解决：国庆前夕，大唐芙蓉园景区为了提高服务质量，想尽可能美化每一个角落，给游客美的享受．如图3， $△ A B O$ 是景区东门的广场一角， $O A ，$ $O B$ 两面墙互相垂直，景区管理部门设计将 $O A$ ， $O B$ 墙面布置成历史人文宣传墙， $A B$ 边上用建筑隔板搭出 $A D$ 段将该角落与广场其他区域隔开， $A D$ 段布置成长安八景图，剩余 $B D$ 部分为广场角出入口，内部空间放置一些绿植和供游人休息的桌椅，考虑到出入安全，还需在靠近出入口的 $E$ 处建一个安检点．已知 $A D = O A = 16 m$ ， $O B = 12 m$ ， $B C$ 平分 $∠ O B A$ ，安检点 $E$ 在 $B C$ 与 $O D$ 的交点处．求点 $E$ 分别到 $O B$ ， $O A$ 墙面的距离。

查看试题解析

五、综合题

16. 在平面直角坐标系 $x O y$ 中，对于 $M, N$ 两点，若在 $y$ 轴上存在点 $T$ ，使得 $∠ M T N = 90 °$ ，且 $M T = N T$ ，则称 $M, N$ 两点互相等垂，其中一个点叫做另一个点的等垂点．已知 $A$ 点的坐标是 $(2, 0)$ ．

(1)、如图①，在点 $B (2, - 2), C (0, 1), D (- 2, 0)$ 中，点 $A$ 的等垂点是（选填“ $B$ ”，“ $C$ ”或“ $D$ ”）

(2)、如图②，若一次函数 $y = 2 x - 1$ 的图象上存在点 $A$ 的等垂点 $A^{'}$ ，求 $A^{'}$ 点的坐标；

(3)、若一次函数 $y = k x + b (k \neq 0)$ 的图象上存在无数个点 $A$ 的等垂点，试写出该一次函数的所有表达式：．

查看试题解析