【培优版】浙教版数学八上5.5 一次函数的简单应用同步练习

试卷更新日期：2024-10-29 类型：同步测试

进入出卷网下载

一、选择题

1. 一辆快车和一辆慢车将一批物资从甲地运往乙地，其中快车送达后立即沿原路返回，且往返速度的大小不变，两车离甲地的距离y(单位：km)与慢车行驶时间t(单位：h)的函数关系如图，则两车先后两次相遇的间隔时间是 (　　)

A、 $\frac{5}{3} h$ B、 $\frac{3}{2} h$ C、 $\frac{7}{5} h$ D、 $\frac{4}{3}$

查看试题解析
2. 弹簧秤中弹簧的长度 $y (c m)$ 与所挂物体的质量 $x (k g)$ 的对应关系如图所示，则这个弹簧秤不挂物体时弹簧的长度为( )

A、 $12 c m$
B、 $11 c m$
C、 $10 c m$
D、 $9 c m$

查看试题解析
3. 生物学研究表明，某种蛇在一定生长阶段，其体长 $y (c m)$ 是尾长 $x (c m)$ 的一次函数，部分数据如下表所示，则 $y$ 与 $x$ 之间的关系式为（）
尾长 $x (c m)$
6
8
10
体长 $y (c m)$
45.5
60.5
75.5

A、 $y = 7.5 x + 0.5$ B、 $y = 7.5 x - 0.5$ C、 $y = 15 x$ D、 $y = 15 x + 45.5$

查看试题解析

4. 珍珍的爸爸是某单位的一名销售员，他的月工资（基本工资＋计件提成）总额随月销售量x（件）的变化而变化，下表是他应得工资w（元）与x之间的关系：

销售量x（件）	100	110	120	130	…
月工资总额w（元）	$2800 + 1000$	$2800 + 1100$	$2800 + 1200$	$2800 + 1300$	…

求珍珍爸爸的月收入不低于5000元时应销售件数的取值范围，有如下解题方法：

方法一：

建立w与x的函数关系式： $w = 100 x + 2800$ ．

由 $w \geq 5000$ ，求得x的范围．

方法二：

月工资因计件提成不同而不同，

$5000 - 2800 = 2200$ ．

由 $10 x \geq 2200$ ，求得x的范围．

下列判断正确的是（）．

A、方法一的思路正确，函数表达式也正确 B、方法一的思路和函数表达式都不正确 C、方法二的思路正确，所列不等式也正确 D、方法二的思路和所列不等式都不正确

查看试题解析

5. 如图，点A ， B ， C在一次函数 $y = - 2 x + m$ 的图象上，它们的横坐标依次为 $- 1$ ， $1$ ， $2$ ，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（　　）

A、 $3$ B、 $1$ C、 $3 (m - 1)$ D、 $\frac{3}{2} (m - 2)$

查看试题解析
6. 古秤是一种人类智慧的产物，也是华夏文明的瑰宝之一．如图，我们可以用秤砣到秤纽（秤杆上手提的部分）的水平距离得出秤钩上所挂物体的重量，称重时，若秤钩所挂物重为x（斤），秤砣到秤纽的水平距离为 $y (c m)$ ．下表中为若干次称重时所记录的一些数据：
x（斤）
1
2
3
4
5
6
y（厘米）
0.75
1
1.25
1.5
1.75
2
当x为11斤时，对应的水平距离y为（）

A、3cm B、3.25cm C、3.5cm D、3.75cm

查看试题解析
7. $《$ 九章算术 $》$ 记载：今有坦高九尺，瓜生其上，蔓日长七寸；瓠生其下，蔓日长一尺 $.$ 问几何日相逢？意思是有一道墙，高 $9$ 尺，在墙头种一株瓜，瓜蔓沿墙向下每天长 $7$ 寸；同时地上种着瓠沿墙向上每天长 $1$ 尺，问瓜蔓、瓠蔓要多少天才相遇？小南绘制如图的函数模型解决了此问题 $.$ 图中 $ℎ ($ 单位：尺 $)$ 表示瓜蔓与瓠蔓离地面的高度， $x ($ 单位：天 $)$ 表示生长时间 $.$ 根据小南的模型，点 $P$ 的横坐标和点 $A$ 的实际意义分别是（）

A、 $\frac{9}{8}$ ，点 $A$ 表示瓜蔓枯萎 B、 $\frac{9}{17}$ ，点 $A$ 表示瓜蔓垂到地面 C、 $\frac{90}{17}$ ，点 $A$ 表示瓜蔓垂到地面 D、 $\frac{16}{3}$ ，点 $A$ 表示瓠蔓垂到地面

查看试题解析
8. 某网红店生产并销售一种特色食品，每天均能限量生产并销售完毕，如图中的线段 $A B$ ， $O C$ 分别表示某天生产成本 $y_{1}$ （单位：元），收入 $y_{2}$ （单位：元）与产量x（单位：千克）之间的函数关系．根据图象信息可知，该网红店某一天中盈利120元时的产量是（）

A、30千克 B、42千克 C、45千克 D、48千克

查看试题解析

二、填空题

9. 在同一直线上，甲骑自行车，乙步行，分别由 $A$ ， $B$ 两地同时向右匀速出发，当甲追上乙时，两人同时停止行驶 $.$ 如图表示两人之间的距离 $y (k m)$ 与所经过的时间 $t (ℎ)$ 之间的函数关系图象，观察图象，出发后 $ℎ$ 甲追上乙；若乙的速度为 $8 k m / ℎ$ ，则经过 $1.5 ℎ$ 甲行驶的路程为．

查看试题解析
10. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系式；折线B﹣C﹣D﹣表示轿车离甲地距离y（千米）与x（小时）之间的函数关系，则货车出发小时与轿车相遇．

查看试题解析
11. 某超市糯米的价格为 5 元/千克，端午节推出促销活动：一次购买的数量不超过 2 千克时，按原价售出，超过 2 千克时，超过的部分打八折．若某人付款 14 元，则他购买了千克糯米；设某人的付款金额为 $x$ 元，购量为 $y$ 千克，则购买量 $y$ 关于付款金额 $x (x > 10)$ 的函数解析式为

查看试题解析
12. 已知合肥到芜湖的距离为 $150$ 千米，现有一辆邮政车往返两城市之间，该邮政车每次到达合肥或芜湖后，均需停留 $1$ 小时再重新出发．暑假期间，合肥某旅游公司计划在同线路上加开一辆旅游大巴车，在试运行期间，该邮政车与旅游大巴车同时从合肥出发，两辆车均保持匀速行驶，经过 $\frac{19}{6}$ 小时两车第一次相遇．两车之间的距离 $s$ 千米与行驶时间 $t$ 小时之间的部分函数关系如图所示．已知行驶过程时，邮政车的速度大于旅游大巴车的速度，请完成以下探究：

(1)、邮政车的速度为千米 $/$ 小时；

(2)、当两车第一次在行驶的路上相遇时，相遇点到合肥的距离为千米．

查看试题解析

三、解答题

13. 某手机专卖店销售 $5$ 部甲型手机和 $8$ 部乙型手机的利润为 $1600$ 元，销售 $15$ 部甲型手机和 $6$ 部乙型手机的利润为 $3000$ 元．

(1)、求每部甲型手机和乙型手机的利润；

(2)、该专卖店计划购进这两种型号的手机共 $120$ 部，其中乙型手机的进货量不低于甲型手机的 $2$ 倍 $.$ 设购进甲型手机 $x$ 部，这 $120$ 部手机全部销售的总利润为 $y$ 元．
$①$ 求 $y$ 关于 $x$ 的函数关系式，并写出 $x$ 的取值范围；
$②$ 该商店如何进货才能使销售总利润最大？

查看试题解析
14. 如图（1），B地在A地的正东方向，某一时刻，乙车从B地开往A地，1小时后，甲车从A地开往B地，当甲车到达B地的同时乙车也到达A地.如图（2），横轴x（小时）表示两车的行驶时间（从乙车出发的时刻开始计时），纵轴y（千米）表示两车与A地的距离.

问题：

(1)、A、B两地相距千米；

(2)、 $l_{1}$ 和 $l_{2}$ 两段线分别表示两车距A地的距离y（千米）与行驶时间x（小时）之间的关系，请问：表示甲车的图象为，表示乙车的图象为；

(3)、求两车相遇时距A地多少千米？

查看试题解析

四、实践探究题

15. 【综合实践】新能源汽车多数采用电能作为动力来源，不需要燃烧汽油，这样就减少了二氧化碳等气体的排放，从而达到保护环境的目的．
【实验操作】为了解汽车电池需要多久能充满，以及充满电量状态下电动汽车的最大行驶里程，某综合实践小组设计两组实验．
实验Ⅰ：探究电池充电状态下电动汽车仪表盘增加的电量 $y (%)$ 与时间t（分钟）的关系，数据记录如表1：
电池充电状态
时间t（分钟）
0
10
30
60
增加的电量 $y (%)$
0
10
30
60
实验Ⅱ：探究充满电量状态下电动汽车行驶过程中仪表盘显示剩余电量 $e (%)$ 与行驶里程s（千米）的关系，数据记录如表2：
汽车行驶过程
已行驶里程s（千米）
0
160
200
280
显示剩余电量 $e (%)$
100
60
50
30
【建立模型】（1）观察表1、表2发现都是一次函数模型，请结合表1、表2的数据，直接写出函数关系式（不写自变量的取值范围）．
y关于t的函数表达式为____________，e关于s的函数表达式为_____________；
【解决问题】（2）某电动汽车在充满电量的状态下，从A地出发前往距出发点480千米的B地，在途中服务区进行一次充电后继续行驶，其已行驶里程数（s）和显示剩余电量（e）的函数关系如下图所示：
①该车到达B地时，显示剩余电量e的值为____________；该车进入服务区充电前显示剩余电量e的值为_____________．
②该车中途充电用了多少分钟？
③当汽车显示剩余电量e的值为60时，该车距出发点A地多少千米？

查看试题解析

16. 根据以下素材，探索完成任务.

如何确定木板分配方案？
素材1	某校开展爱心义卖活动，小艺和同学们打算推销自己的手工制品.他们以每张15元的价格买了100张矩形木板，每张木板长和宽分别为 80cm，40 cm.
素材2	如图①，现将部分木板按虚线裁剪，剪去四个边长相同的小正方形（阴影部分）.把剩余五个矩形拼制成无盖长方体收纳盒，使其底面长与宽之比为3：1.如图②，其余木板按虚线裁木板（阴影部分是余料），剪出两块给部分盒子配上盖子。
素材3	售价如标签所示：
问题解决
任务1	计算盒子高度	求出长方体收纳盒的高度.
任务2	确定分配方案1	若制成的有盖收纳盒个数大于无盖收纳盒，但不到无盖收纳盒个数的2倍，木板该如何分配？请给出分配方案.
任务3	确定分配方案2	在任务2的条件下，为了提高利润，小艺打算把图②裁剪下来的余料（阴影部分）利用起来，一张矩形余料可以制成一把小木剑，并以5元/个的价格销售.请确定木板分配方案，使销售后获得最大利润.

查看试题解析

五、综合题

17. 某动力科学研究院实验基地内装有一段笔直的轨道 $A B$ ，长度为 $1 m$ 的金属滑块在上面做往返滑动．如图，滑块首先沿 $A B$ 方向从左向右匀速滑动，滑动速度为 $9 m / s$ ，滑动开始前滑块左端与点 $A$ 重合，当滑块右端到达点 $B$ 时，滑块停顿 $2 s$ ，然后再以小于 $9 m / s$ 的速度匀速返回，直到滑块的左端与点 $A$ 重合，滑动停止．设时间为 $t (s)$ 时，滑块左端离点 $A$ 的距离为 $l_{1} (m)$ ，右端离点 $B$ 的距离为 $l_{2} (m)$ ，记 $d = l_{1} - l_{2} ， d$ 与 $t$ 具有函数关系．已知滑块在从左向右滑动过程中，当 $t = 4.5 s$ 和 $5.5 s$ 时，与之对应的 $d$ 的两个值互为相反数；滑块从点 $A$ 出发到最后返回点 $A$ ，整个过程总用时 $27 s$ （含停顿时间）．请你根据所给条件解决下列问题：

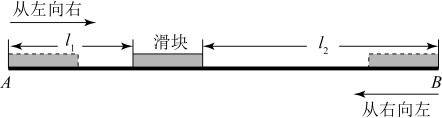(1)、滑块从点 $A$ 到点 $B$ 的滑动过程中， $d$ 的值；（填“由负到正”或“由正到负”）

(2)、滑块从点 $B$ 到点 $A$ 的滑动过程中，求 $d$ 与 $t$ 的函数表达式；

(3)、在整个往返过程中，若 $d = 18$ ，求 $t$ 的值．

查看试题解析

电池充电状态
时间t（分钟）	0	10	30	60
增加的电量 $y (%)$	0	10	30	60

汽车行驶过程
已行驶里程s（千米）	0	160	200	280
显示剩余电量 $e (%)$	100	60	50	30

尾长 $x (c m)$	6	8	10
体长 $y (c m)$	45.5	60.5	75.5

x（斤）	1	2	3	4	5	6
y（厘米）	0.75	1	1.25	1.5	1.75	2