山东省济宁市微山县2017年中考数学二模试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. 与﹣1的和等于零的数是( )A、﹣1 B、0 C、1 D、2. 下列各式从左到右的变形正确的是( )A、﹣2x+4y=﹣2(x﹣4y) B、a2﹣6=(a+2)(a﹣3) C、(a+b)2=a2+b2 D、x2﹣y2=(x﹣y)(x+y)3. 如图,直线AD∥BC,点C,D,E在同一条直线上,∠ADE的角平分线DG与直线AD的垂线(垂足为点F)相交于点G,若∠G=25°,则∠1的度数是( )
 A、50° B、30° C、25° D、15°4. 今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )A、总体 B、个体 C、一个样本 D、样本容量5. 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,▱ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
A、50° B、30° C、25° D、15°4. 今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )A、总体 B、个体 C、一个样本 D、样本容量5. 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,▱ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( ) A、 B、 C、 D、6. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )
A、 B、 C、 D、6. 一个几何体的三视图如图所示,则这个几何体的侧面积是( ) A、4π B、2π C、4 D、π7. 一元二次方程(k﹣2)x2+kx+2=0(k≠2)的根的情况是( )A、该方程有两个不相等的实数根 B、该方程有两个相等的实数根 C、该方程有实数根 D、该方程没有实数根8. 如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=100°,则∠DCE的度数为( )
A、4π B、2π C、4 D、π7. 一元二次方程(k﹣2)x2+kx+2=0(k≠2)的根的情况是( )A、该方程有两个不相等的实数根 B、该方程有两个相等的实数根 C、该方程有实数根 D、该方程没有实数根8. 如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=100°,则∠DCE的度数为( )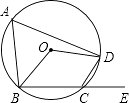 A、40° B、60° C、50° D、80°9. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac﹣b2<2a;④2b=3a.
A、40° B、60° C、50° D、80°9. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac﹣b2<2a;④2b=3a.其中正确的结论是( )
 A、①③ B、②④ C、①④ D、②③10. 如图是用大小相同的正方形摆放成的一组有规律的图案,图案一需要2个正方形;图案二需要5个正方形;图案三需要10个正方形;图案四需要17个正方形;…按此规律摆下去,图案三十需要正方形个数是( )
A、①③ B、②④ C、①④ D、②③10. 如图是用大小相同的正方形摆放成的一组有规律的图案,图案一需要2个正方形;图案二需要5个正方形;图案三需要10个正方形;图案四需要17个正方形;…按此规律摆下去,图案三十需要正方形个数是( )

A、902 B、901 C、900 D、899二、填空题
-
11. 计算 ×( )﹣1+(sin60°+π)0的结果等于 .12. 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)
 13. 如图,直线y= x+b与双曲线y= 相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是 .
13. 如图,直线y= x+b与双曲线y= 相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是 . 14. 已知a、b是一元二次方程x2﹣x﹣2018=0的两个实数根,则代数式a2﹣2a﹣b的值等于 .15. 如图,将边长分别为6,2 的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是(只填序号)
14. 已知a、b是一元二次方程x2﹣x﹣2018=0的两个实数根,则代数式a2﹣2a﹣b的值等于 .15. 如图,将边长分别为6,2 的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是(只填序号)
三、解答题
-
16. 先化简再求值:( ﹣x﹣1)÷(2﹣ ),其中x2﹣2x﹣3=0.17. 已知:如图,AD=BC,AC=BD.猜想AE与BE的数量关系并证明.
 18. 雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:
18. 雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:类别
雾霾天气的主要成因
百分比
A
工业污染
45%
B
汽车尾气排放
m
C
城中村燃煤问题
15%
D
其他(绿化不足等)
n
 (1)、请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;(2)、若该市有800万人口,请你估计持有B,C两类看法的市民共有多少人?(3)、小明同学在四个质地、大小、形状都完全相同的小球上标记A,B,C,D代表四个雾霾天气的主要成因中,放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求出小颖同学刚好抽到B和D的概率.(用A,B,C,D表示各项目)19. 为加快建设经济强、环境美、后劲足、群众富的实力微山,魅力微山,活力微山,幸福微山;聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶甲、乙两贫困村的计划,现决定从某地运送1225箱鱼苗到甲、乙两村养殖.若用大、小货车共20辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力和其运往甲、乙两村的运费如表:
(1)、请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;(2)、若该市有800万人口,请你估计持有B,C两类看法的市民共有多少人?(3)、小明同学在四个质地、大小、形状都完全相同的小球上标记A,B,C,D代表四个雾霾天气的主要成因中,放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求出小颖同学刚好抽到B和D的概率.(用A,B,C,D表示各项目)19. 为加快建设经济强、环境美、后劲足、群众富的实力微山,魅力微山,活力微山,幸福微山;聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶甲、乙两贫困村的计划,现决定从某地运送1225箱鱼苗到甲、乙两村养殖.若用大、小货车共20辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力和其运往甲、乙两村的运费如表:车型
载货能力(箱/辆)
运费
甲村(元/辆)
乙村(元/辆)
大货车
70
800
900
小货车
35
400
600
(1)、求这20辆车中大、小货车各多少辆?(2)、现安排其中16辆货车前往甲村,其余货车前往乙村,设前往甲村的大货车为x辆,前往甲、乙两村总费用为y元,试求出y与x的函数解析式及x的取值范围;(3)、在(2)的条件下,若运往甲村的鱼苗不少于980箱,请你写出使总费用最少的货车调配方案,并求出最少费用.20. 如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E,F,连接EF. (1)、求证:BC是⊙O的切线;(2)、若FC=2,求PC的长.21. 【阅读新加】
(1)、求证:BC是⊙O的切线;(2)、若FC=2,求PC的长.21. 【阅读新加】①1.按一定顺序排列的一列数称为数列,记作:{an}(n属于正整数),数列中的每一个数都叫做这个数列的项,排在第一位的数称为这个数列的第1项(通常也叫做首项),记作:a1;排在第二位的数称为这个数列的第2项,记作:a2;…;排在第n位的数称为这个数列的第n项,记作:an .
②2.等比数列(又名几何数列),是一种特殊数列,如果一个数列从第二项起,每一项与它的前一项的比等于同一常数,这个数列就叫做等比数列.因为第二项与第一项的比和第三项与第二项的比相等.这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),注:q=1时,an为常数列.
例如:数列1,﹣3,9,﹣27,81是等比数列,公比q=3.
由定义可知:如果数列a1 , a2 , a3 , …,an…是等比数列,
那么a2÷a1=d,a3÷a2=d,an÷an﹣1=d.
即a2=a1d,a3=a1dd=a1d2 , ….
【应用新知】
(1)、等比数列10,10,10,10,10,10的公比是 .(2)、如果等比数列{an}的首项为a1 , 公比为q(q≠0).那么这个数列的第n项an等于 . (用含a1 , q的代数式表示)(3)、已知实数a1 , a2 , a3 , a4 , a5 , a6 , a7依次成等比数列,已知a1=3,a7=192,求a4 .22. 如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等. (1)、求双曲线和抛物线的解析式;(2)、计算△ABC的面积;(3)、如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求双曲线和抛物线的解析式;(2)、计算△ABC的面积;(3)、如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.