内蒙古鄂尔多斯市东胜区2017年中考数学一模试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. ﹣ 的倒数的相反数等于( )A、﹣2 B、 C、﹣ D、22. 把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )
 A、祝 B、你 C、顺 D、利3. 下列计算正确的是( )A、x2+x2=x4 B、x2y﹣2x2y=﹣x2y C、(3x)2=3x2 D、x2•x3=x64. 如图,已知AB∥CD,∠C=65°,∠E=30°,则∠A的度数为( )
A、祝 B、你 C、顺 D、利3. 下列计算正确的是( )A、x2+x2=x4 B、x2y﹣2x2y=﹣x2y C、(3x)2=3x2 D、x2•x3=x64. 如图,已知AB∥CD,∠C=65°,∠E=30°,则∠A的度数为( )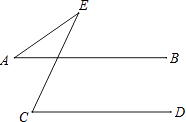 A、30° B、32.5° C、35° D、37.5°5. 在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )A、平均数为160 B、中位数为158 C、众数为158 D、方差为20.36. 某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为( )A、 B、 C、 D、7. 施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是( )
A、30° B、32.5° C、35° D、37.5°5. 在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )A、平均数为160 B、中位数为158 C、众数为158 D、方差为20.36. 某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为( )A、 B、 C、 D、7. 施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是( )
A、 ﹣ =2 B、 ﹣ =2 C、 ﹣ =2 D、 ﹣ =28. 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( ) A、24﹣4π B、32﹣4π C、32﹣8π D、169. 已知下列命题中为真命题的是( )
A、24﹣4π B、32﹣4π C、32﹣8π D、169. 已知下列命题中为真命题的是( )① 的算术平方根是4;
②若ma2>na2 , 则m>n;
③正八边形的一个内角的度数是135°;
④对角线互相垂直平分的四边形是菱形;
⑤平分弦的直径垂直于弦.
A、①③④ B、②③⑤ C、①④⑤ D、②③④10. 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( ) A、
A、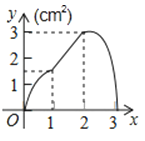 B、
B、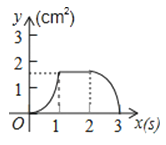 C、
C、 D、
D、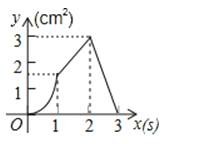
二、填空题
-
11. 函数 中,自变量x的取值范围 .12. 2016年我市财政收入451亿元,请使用科学记数法表示451亿元为元.13. 新定义运算“*”,规定x*y=x2+y,若﹣1*2=k,则k能否使得一元二次方程x2﹣2kx+9=0有两个相等的实数解(填“能”或‘否’).14. 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=4,BC=6,则FD的长为 .
 15. 等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .
15. 等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .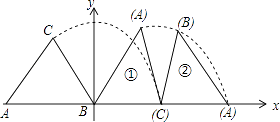 16. 将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有95个“○”,则n= .
16. 将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有95个“○”,则n= .
三、解答题
-
17. 综合题
(1)、先解不等式组 ,然后判断 是不是此不等式组的一个整数解.(2)、化简求值:先化简 ,再从1,2,3中选取一个适当的数代入求值.18. 为了调查学生对雾霾天气的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.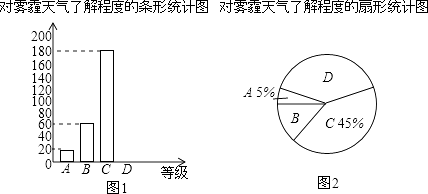
对雾霾的了解程度
百分比
A.非常了解
5%
A.比较了解
15%
C.基本了解
45%
D.不了解
n
请结合统计图表,回答下列问题:
(1)、本次参与调查的学生共有人,n=;扇形统计图中D部分扇形所对应的圆心角是度;(2)、请补全条形统计图;(3)、根据调查结果,学校准备开展关于雾霾的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去,否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.19. 如图,已知一次函数y=kx+b的图象交反比例函数 图象于点A,B,交x轴于点C. (1)、求m的取值范围;(2)、若点A的坐标是(1,﹣4),且 ,求m的值和一次函数的解析式;(3)、在(2)的情况下,请直接写出不等式 的解集.20. 如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)、求m的取值范围;(2)、若点A的坐标是(1,﹣4),且 ,求m的值和一次函数的解析式;(3)、在(2)的情况下,请直接写出不等式 的解集.20. 如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC. (1)、求证:OE=OF;(2)、若BC=2 ,求AB的长.21. 如图,海中有一小岛P,在距小岛16 海里范围内有暗礁,一轮船自西向东航行,它在A处测得小岛P位于北偏东45°,且A,P之间的距离为32海里,若轮船继续向正东方向航行,有无触礁的危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向改变航向,才能安全通过这一海域?
(1)、求证:OE=OF;(2)、若BC=2 ,求AB的长.21. 如图,海中有一小岛P,在距小岛16 海里范围内有暗礁,一轮船自西向东航行,它在A处测得小岛P位于北偏东45°,且A,P之间的距离为32海里,若轮船继续向正东方向航行,有无触礁的危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向改变航向,才能安全通过这一海域? 22. 如图,四边形ABCD是平行四边形,点A、B、C在☉O上,AD与⊙O相切,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,且∠PCB=2∠BAF.
22. 如图,四边形ABCD是平行四边形,点A、B、C在☉O上,AD与⊙O相切,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,且∠PCB=2∠BAF.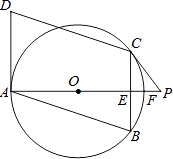 (1)、求证:直线PC是⊙O的切线;(2)、若AB= ,AD=2,求线段PC的长.23. 春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.24. 如图1,对称轴为直线x= 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
(1)、求证:直线PC是⊙O的切线;(2)、若AB= ,AD=2,求线段PC的长.23. 春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.24. 如图1,对称轴为直线x= 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A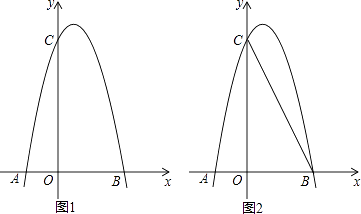 (1)、求抛物线的解析式;(2)、若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;(3)、如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;(3)、如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.