人教版数学九年级全册知识点训练营——圆幂定理模型

试卷更新日期：2024-10-28 类型：复习试卷

进入出卷网下载

一、切割线定理模型

1. 如图， $A B$ 为 $⊙ O$ 的直径， $C D$ 与 $⊙ O$ 相切于点C ，交 $B A$ 的延长线于点D ，若 $∠ B = 30 °$ ， $A D = 3$ ，则线段 $A B$ 的长是（）

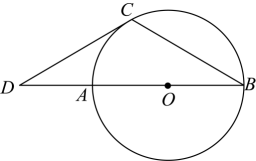A、3 B、4 C、5 D、6

查看试题解析
2. 筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理：如图（1），其原理是利用流动的河水，水斗舀满河水，将水提升，水流源源不断，流入田地（2），筒车圆O与水面分别交于点A、B，筒车上均匀分布着若干盛水筒，接水槽 $M N$ 所在的直线是圆O的切线，且与直线 $A B$ 交于点M，P、O、C三点共线， $P C$ 是圆O的直径时；

(1)、求证： $∠ B A P = ∠ M P B$ ；

(2)、求证： $M P^{2} = M A \cdot M B$ ；

(3)、若 $A B = A P$ ， $M B = 8$ ， $M P = 12$ ，求 $B P$ 的长

查看试题解析
3. 如图， $B D$ 是 $⊙ O$ 的直径，A是 $B D$ 延长线上的一点，点E在 $⊙ O$ 上， $B C ⊥ A E$ ，交 $A E$ 的延长线于点C， $B C$ 交 $⊙ O$ 于点F，且点E是 $\overset{⌢}{D F}$ 的中点．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、若 $A D = 3 ， A E = 3 \sqrt{2}$ ，求 $⊙ O$ 的半径．

查看试题解析

二、相交弦定理模型

4. 如图，已知AB为⊙O的直径，C为⊙O上一点，CD⊥AB于D，AD=9，BD=4，以C为圆心，CD为半径的圆与⊙O相交于P，Q两点，弦PQ交CD于E，则PE•EQ的值是（）

A、24 B、9 C、6 D、27

查看试题解析
5. 如图，⊙O的弦AB，CD相交于点P，若AP=6，BP=8，CP=4，则CD长为（）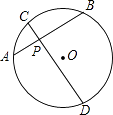

A、16 B、24 C、12 D、不能确定

查看试题解析
6. 已知四边形ABCD两条对角线相交于点E，AB＝AC＝AD，AE＝3，EC＝1，则BE•DE的值为（）

A、6 B、7 C、12 D、16

查看试题解析
7. 如图所示，动点C在⊙O的弦AB上运动，AB=2 $\sqrt{3}$ ，连接OC，CD⊥OC交⊙O于点D.则CD的最大值为.

查看试题解析
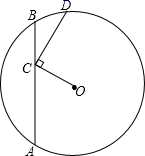8. 如图，已知⊙O中，弦AB与CD相交于点P．
求证：PA•PB=PC•PD．

查看试题解析
9. 如图， $△ A B C$ 内接于⊙ $O$ ， ⊙ $O$ 的直径AD与弦BC相交于点E，BE＝CE，过点D作 $D F ∥ B C$ 交AC的延长线于点F．

(1)、求证：DF是⊙ $O$ 的切线；

(2)、若 $s i n ∠ B A D = \frac{1}{3}$ ， AB＝6，求DF的长．

查看试题解析
10. 如图，AB为⊙O的直径，点E在⊙O上，C为 $\overset{⌢}{B E}$ 的中点，过点C作直线CD⊥AE于D，连接AC、BC.

(1)、试判断直线CD与⊙O的位置关系，并说明理由；

(2)、若AD＝2，AC＝ $\sqrt{6}$ ，求AB的长.

查看试题解析
11. 阅读下面材料，完成（1）～（3）题.
数学课上，老师出示了这样一道题：

如图1，△ABC中，AC＝BC＝a，∠ACB＝90°，点D在AB上，且AD＝kAB（其中0＜k＜ $\frac{1}{2}$ ），直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E，探究线段DC、DE的数量关系，并证明.

同学们经过思考后，交流了自己的想法：

小明：“通过观察和度量，发现DC与DE相等”；

小伟：“通过构造全等三角形，经过进一步推理，可以得到DC与DE相等”

小强：“通过进一步的推理计算，可以得到BE与BC的数量关系”

老师：“保留原题条件，连接CE交AB于点O.如果给出BO与DO的数量关系，那么可以求出CO•EO的值”

(1)、在图1中将图补充完整，并证明DC＝DE；

(2)、直接写出线段BE与BC的数量关系（用含k的代数式表示）；

(3)、在图2中将图补充完整，若BO＝ $\frac{5}{13}$ DO，求CO•EO的值（用含a的代数式表示）.

查看试题解析

三、割线定理

12. 如图，A、B、C、D为⊙O上的点，直线BA与DC相交于点P，PA=2，PC=CD=3，则PB=（）

A、6 B、7 C、8 D、9

查看试题解析
13. 已知：如图， $P A B$ 、 $P C D$ 是⊙ $O$ 的割线， $P A = 4 c m$ ， $A B = 6 c m$ ， $C D = 3 c m$ .则 $P D$ = $c m$ .

查看试题解析
14. 如图，延长弦 $D B$ 、弦 $E C$ ，交于圆外一点A，连接 $C D$ 、 $B E$ .

(1)、证明： $△ A C D ∽ △ A B E$ ；

(2)、若 $A B = 5$ ， $A C = 6$ ， $A D = 12$ ，求 $A E$ .

查看试题解析
15. 如图，P为⊙O外的一点，过点P作⊙O的两条割线，分别交⊙O于A、B和C、D，且AB是⊙O的直径，已知PA=OA=4，AC=CD．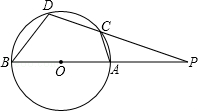

(1)、求DC的长；

(2)、求cosB的值．

查看试题解析
16. 我们知道，直线与圆有三种位置关系：相交、相切、相离.当直线与圆有两个公共点（即直线与圆相交）时，这条直线就叫做圆的割线.割线也有一些相关的定理.比如，割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等.下面给出了不完整的定理“证明一”，请补充完整.

已知：如图①，过 $⊙ O$ 外一点 $P$ 作 $⊙ O$ 的两条割线，一条交 $⊙ O$ 于 $A$ 、 $B$ 点，另一条交 $⊙ O$ 于 $C$ 、 $D$ 点.
求证： $P A \cdot P B = P C \cdot P D$ .
证明一：连接 $A D$ 、 $B C$ ，
∵ $∠ A$ 和 $∠ C$ 为 $\overset{⌢}{B D}$ 所对的圆周角，∴_▲_.
又∵ $∠ P = ∠ P$ ，∴_▲_，∴_▲_.
即 $P A \cdot P B = P C \cdot P D$ .
研究后发现，如图②，如果连接 $A C$ 、 $B D$ ，即可得到学习过的圆内接四边形 $A B D C$ .那么或许割线定理也可以用圆内接四边形的性质来证明.请根据提示，独立完成证明二.
证明二：连接 $A C$ 、 $B D$ ，

查看试题解析